当前位置：试卷中心 > 试卷详情

2023-2024学年江苏省泰州市名校高三（上）期初数学试卷

发布：2024/8/2 8:0:9

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A={1，2，3}，
B
=
{
x
|
x
-
2
x
≤
0
，
x
∈
Z
}
，则A∪B=（　　）
A．{1，2} B．{0，1，2，3} C．{1，2，3} D．{0，1，2}
组卷：171引用：8难度：0.7
解析
2．已知复数
z
=
2
-
i
3
+
4
i
，则
|
z
|
=（　　）
A．
5
B．
5
5
C．
1
5
D．
2
2
组卷：194引用：5难度：0.7
解析
3．已知等比数列{a_n}的前n项和为S_n，且2S₃，3S₅，4S₆成等差数列，则数列{a_n}的公比q=（　　）
A．1或
-
1
2
B．-1或
1
2
C．-1或2 D．1或-2
组卷：129引用：6难度：0.7
解析
4．若双曲线ky²-8x²=8的焦距为6，则该双曲线的离心率为（　　）
A．
3
2
4
B．
3
2
C．3 D．
10
3
组卷：138引用：5难度：0.7
解析
5．向量旋转具有反映点与点之间特殊对应关系的特征，在电子信息传导方面有重要应用．平面向量旋转公式在中学数学中用于求旋转相关点的轨迹方程具有明显优势，已知对任意平面向量
AB
=
（
x
,
y
）
，把
AB
绕其起点沿逆时针方向旋转θ角得到向量
AP
=
（
xcosθ
-
ysinθ
，
xsinθ
+
ycosθ
）
，叫做把点B绕点A沿逆时针方向旋转θ角得到点P．已知平面内点A（1，2），点
B
（
1
+
2
，
2
-
2
2
）
，把点B绕点A沿顺时针方向旋转
π
4
后得到点P，则点P的坐标为（　　）
A．（-2，1） B．（4，1） C．（2，-1） D．（0，-1）
组卷：222引用：6难度：0.6
解析
6．已知cos（α+
π
12
）=
3
5
，α∈（0，
π
2
），则cos（α+
π
3
）=（　　）
A．-
2
10
B．
4
5
C．
3
-
4
3
10
D．
2
10
组卷：859引用：16难度：0.5
解析
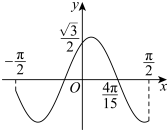7．已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜
π
2
）的部分图象如图所示，则f（π）的值为（　　）
A．
3
2
B．
2
2
C．
1
2
D．-
3
2
组卷：248引用：3难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

21．已知椭圆
x
2
4
+y²=1的左右顶点为A、B，直线l：x=1．已知O为坐标原点，圆G过点O、B交直线l于M、N两点，直线AM、AN分别交椭圆于P、Q．
（1）记直线AM，AN的斜率分别为k₁、k₂，求k₁•k₂的值；
（2）证明直线PQ过定点，并求该定点坐标．
组卷：430引用：10难度：0.6
解析
22．已知函数f（x）=ae^x-e^-x-（a+1）x（a∈R），f（x）既存在极大值，又存在极小值．
（Ⅰ）求实数a的取值范围；
（Ⅱ）当0＜a＜1时，x₁，x₂分别为f（x）的极大值点和极小值点．且f（x₁）+kf（x₂）＞0，求实数k的取值范围．
组卷：325引用：6难度：0.3
解析