当前位置：试卷中心 > 试卷详情

2022-2023学年湖南省长沙市开福区青竹湖湘一外国语学校八年级（上）期中数学试卷

发布：2024/9/23 4:0:8

一、单选题（在下列各题的四个选项中，只有一项是符合题意的。请在答题卡中选择符合题意的选项。本题共10个小题，每小题3分，共30分）

1．下列图标中是轴对称图形的是（　　）
A． B． C． D．
组卷：10引用：1难度：0.8
解析
2．9的相反数是（　　）
A．
1
9
B．9 C．-9 D．-
1
9
组卷：578引用：86难度：0.9
解析

3．下列调查中，适合用全面调查的方式收集数据的是（　　）

A．对某市中小学生每天完成作业时间的调查

B．对全国中学生节水意识的调查

C．对某班全体学生新冠疫苗接种情况的调查

D．对某批次灯泡使用寿命的调查

组卷：133引用：3难度：0.9

解析

4．下列式子：-5x,
1
a
+
b
，
1
2
a
2
-
1
2
b
2
，
3
10
m
，
2
π
，其中分式有（　　）
A．1个 B．2个 C．3个 D．4个
组卷：1285引用：14难度：0.8
解析
5．某市计划在公路l旁修建一个飞机场M，现有如下四种方案，则机场M到A，B两个城市之间的距离之和最短的是（　　）
A． B．
C． D．
组卷：710引用：3难度：0.8
解析
6．（-6xy²）²÷（-3xy）的结果为（　　）
A．-12xy³ B．2y³ C．12xy D．2xy³
组卷：213引用：5难度：0.9
解析
7．将9.5²变形正确的是（　　）
A．9.5²=9²+0.5²
B．9.5²=（10+0.5）（10-0.5）
C．9.5²=10²-2×10×0.5+0.5²
D．9.5²=9²+9×0.5+0.5²
组卷：816引用：38难度：0.8
解析
8．如图所示，在△ABC中，D，E分别是边AC，BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数为（　　）
A．15° B．20° C．25° D．30°
组卷：2881引用：43难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共9小题，17、18、19小题6分每题，20、21题8分每题，22、23题9分每题，24、25题10分每题）

24．阅读理解并填空：
（1）为了求代数式x²+2x+3的值，我们必须知道x的值．
若x=1，则这个代数式的值为
；若x=2，则这个代数式的值为
；……
可见，这个代数式的值因x的取值不同而变化，尽管如此，我们还是有办法来考虑这个代数式的值的范围．
（2）把一个多项式进行部分因式分解可以解决求代数式的最大（或最小）值问题．
例如：x²+2x+3=x²+2x+1+2=（x+1）²+2，因为（x+1）²是非负数，所以这个代数式的最小值是
，此时相应的x的值是
．
（3）求代数式-x²-6x+12的最大值，并写出相应的x的值．
（4）试探究关于x、y的代数式5x²-4xy+y²+6x+25是否有最小值，若存在，求出最小值及此时x、y的值；若不存在，请说明理由．
组卷：378引用：1难度：0.5
解析
25．如图1，等腰直角△ABC中，∠ACB=90°，CB=CA，线段ED经过点C，过A作AD⊥ED于点D，过B作BE⊥ED于E．

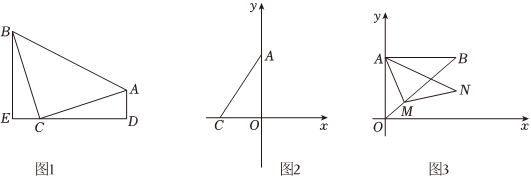
（1）求证：△BEC≌△CDA．
（2）如图2，已知在平面直角坐标系xOy中，O为坐标原点，点A的坐标为（0，8），点C的坐标为（-6，0），点B是第二象限中的一点，若△ABC是以AC为直角边的等腰直角三角形，求点B的坐标；
（3）如图3，已知在平面直角坐标系xOy中，O为坐标原点，在等腰直角△OAB中，∠OAB=90°，OA=AB=8，点M在线段OB上从O向B运动（运动到点B停止），以点M为直角顶点向右上方作等腰直角△AMN，求点N移动的距离．
组卷：360引用：3难度：0.4
解析