2022-2023学年云南省昆明市高二（下）期末数学试卷

一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．复平面内，复数z所对应的点为（2，1），则zi=（　　）

  A．2+i

  B．2+2i

  C．-1+2i

  D．-1-2i
  组卷：11引用：1难度：0.7

  解析

• 2．已知集合A={1，2，4}，集合B={a,a+2}，若A∩B=B，则a=（　　）

  A．0

  B． 1 2

  C．1

  D．2
  组卷：108引用：4难度：0.7

  解析

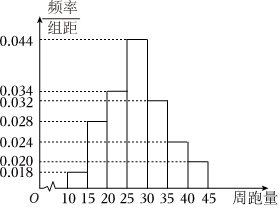• 3．某校为调查学生跑步锻炼的情况，从该校3000名学生中随机抽取300名学生，并统计这300名学生平均每周的跑步量（简称“周跑量”，单位：km/周），得到如图所示的频率分布直方图．称周跑量不少于35km周的学生为“跑步达人”，用频率分布直方图估计这3000名学生中“跑步达人”的人数为（　　）

  A．66

  B．132

  C．660

  D．720
  组卷：175引用：4难度：0.9

  解析

• 4．大西洋鲑鱼每年都要逆流而上，洄游到产卵地产卵．科学家发现鲑鱼的游速v（单位：m/s）与鲑鱼的耗氧量的单位数P的关系为

  v

  =

  1

  2

  lo

  g

  3

  P

  100

  ，则鲑鱼静止时耗氧量的单位数为（　　）

  A．1

  B．100

  C．200

  D．300
  组卷：38引用：2难度：0.7

  解析

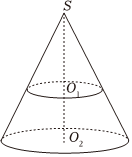• 5．如图，圆锥SO₂被平行于底面的一个平面所截，截去一个上、下底面半径分别为3和5，高为4的圆台O₁O₂，则所得圆锥SO₁的体积为（　　）

  A．16π

  B．18π

  C．20π

  D．24π
  组卷：45引用：2难度：0.7

  解析

• 6．已知椭圆

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  ，

  F

  1

  ，

  F

  2

  分别是C的左，右焦点，P为C上一点，若线段PF₁的中点在y轴上，

  ∠

  P

  F

  1

  F

  2

  =

  π

  6

  ，则C的离心率为（　　）

  A． 3 3

  B． 2 3

  C． 6 3

  D． 2 - 3
  组卷：277引用：1难度：0.6

  解析

• 7．已知

  sin

  （

  π

  6

  -

  x

  ）

  =

  1

  4

  ，则

  sin

  （

  2

  x

  +

  π

  6

  ）

  =（　　）

  A． - 7 8

  B． - 1 8

  C． 1 8

  D． 7 8
  组卷：173引用：2难度：0.7

  解析

四、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知双曲线M：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  过点

  （

  5

  ，

  1

  2

  ）

  ，一条渐近线方程为x-2y=0．
  （1）求M的方程；
  （2）过M的右焦点的直线l与M的右支交于P，Q两点，T（-3，0），若△TPQ的外接圆圆心E在y轴上，求直线l的方程．
  组卷：60引用：1难度：0.6

  解析

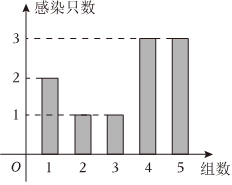• 22．某研究所研究某一型号疫苗的有效性，研究人员随机选取50只小白鼠注射疫苗，并将白鼠分成5组，每组10只，观察每组被感染的白鼠数．现用随机变量X_i（i=1，2，⋯，5）表示第i组被感染的白鼠数，并将随机变量X_i的观测值x₁（i=1，2，⋯，5）绘制成如图所示的频数分布条形图．若接种疫苗后每只白鼠被感染的概率为p（p∈（0，1）），假设每只白鼠是否被感染是相互独立的．记A_i为事件“X_i=x_i（i=1，2，⋯，5）”．
  （1）写出P（A₁）（用p表示，组合数不必计算）；
  （2）研究团队发现概率p与参数θ（0＜θ＜1）之间的关系为

  p

  =

  1

  2

  θ

  2

  -

  5

  6

  θ

  +

  19

  45

  ．在统计学中，若参数θ=θ₀时的p值使得概率P（A₁A₂A₃A₄A₅）最大，称θ₀是θ的最大似然估计，求θ₀．
  组卷：75引用：1难度：0.5

  解析