当前位置：试卷中心 > 试卷详情

2022-2023学年江西省部分学校高一（下）期末数学试卷

发布：2024/6/26 8:0:9

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．已知复数z=1+2i（i为虚数单位），则
z
的虚部为（　　）
A．2 B．-2 C．2i D．-2i
组卷：58引用：3难度：0.9
解析
2．已知平面向量
a
=
（
1
，
0
）
，
b
=
（
1
，
2
）
，若
（
a
+
λ
b
）
⊥
a
，则实数λ=（　　）
A．-1 B．-2 C．
-
1
2
D．1
组卷：185引用：7难度：0.7
解析
3．已知θ∈（
3
π
2
，2π），且cos2θ+cosθ=0，则sin2θ+sinθ等于（　　）
A．0 B．
3
C．
-
3
D．
2
组卷：167引用：3难度：0.6
解析
4．一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱．这个四棱锥的底面为正方形，且底面边长与各侧棱长相等，这个三棱锥的底面边长与各侧棱长也都相等．设四棱锥、三棱锥、三棱柱的高分别为h₁，h₂，h,则h₁：h₂：h=（　　）
A．
3
：
1
：
1
B．
3
：
2
：
2
C．
3
：
2
：
2
D．
3
：
2
：
3
组卷：978引用：11难度：0.9
解析
5．在△ABC中，AC=3，BC=4，∠C=90°．P为△ABC所在平面内的动点，且PC=1，则
PA
•
PB
的取值范围是（　　）
A．[-5，3] B．[-3，5] C．[-6，4] D．[-4，6]
组卷：5628引用：30难度：0.4
解析
6．△ABC的内角A，B，C所对的边分别为a,b,c,且3acosB-3bcosA=2c,则
tan
A
tan
B
的值是（　　）
A．1 B．3 C．4 D．5
组卷：153引用：3难度：0.8
解析
7．已知函数f（x）=4sinωx•sin²（
ωx
2
+
π
4
）-2sin²ωx（ω＞0）在区间[
-
π
2
，
2
π
3
]上是增函数，且在区间[0，π]上恰好取得一次最大值，则ω的取值范围是（　　）
A．（0，1] B．（0，
3
4
] C．[1，+∞） D．[
1
2
，
3
4
]
组卷：532引用：4难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

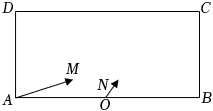21．某大学科研团队在如下图所示的长方形区域ABCD内（包含边界）进行粒子撞击实验，科研人员在A、O两处同时释放甲、乙两颗粒子．甲粒子在A处按
AM
方向做匀速直线运动，乙粒子在O处按
ON
方向做匀速直线运动，两颗粒子碰撞之处记为点P，且粒子相互碰撞或触碰边界后爆炸消失．已知AB长度为6分米，O为AB中点．
（1）已知向量
AM
与
ON
的夹角为
π
3
，且AD足够长．若两颗粒子成功发生碰撞，求两颗粒子运动路程之和的最大值；
（2）设向量
AM
与向量
AO
的夹角为α（0＜α＜π），向量
ON
与向量
OB
的夹角为β（0＜β＜π），甲粒子的运动速度是乙粒子运动速度的2倍．请问AD的长度至少为多少分米，才能确保对任意的β∈（0，π），总可以通过调整甲粒子的释放角度α，使两颗粒子能成功发生碰撞？
组卷：97引用：5难度：0.4
解析
22．已知函数f（x）=x²-a|x|+b,g（x）=cos2x+（2a-1）cosx+1-a（a,b∈R）．
（Ⅰ）判断f（x）的奇偶性并证明；
（Ⅱ）若a=1，x∈[0，π]，求g（x）的最小值和最大值；
（Ⅲ）定义
min
{
x
,
y
}
=
x
,
x
≤
y
y
,
x
＞
y
，设h（x）=min{f（x），g（x）}，若h（x）在
（
-
π
2
，
π
2
）
内恰有三个不同的零点，求a的取值集合．
组卷：56引用：4难度：0.6
解析