2022-2023学年江苏省南通市海安高级中学高一（下）期中数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．设x∈R，则“ln（x-2）＜1”是“x＞2”的（　　）条件．

  A．充分不必要	B．必要不充分
  C．充要	D．既不充分又不必要
  组卷：22引用：2难度：0.7

  解析

• 2．已知集合A={x||x-1|＜1}，B={x|x＜1或x≥4}，则A∪（∁_RB）=（　　）

  A．{x|1＜x＜2}

  B．{x|0＜x＜4}

  C．{x|1≤x＜2}

  D．{x|0＜x≤4}
  组卷：140引用：2难度：0.7

  解析

• 3．已知复数z满足

  1

  +

  3

  i

  z

  =

  3

  +

  4

  i

  ，则

  |

  z

  |

  =（　　）

  A． 2 5 5

  B． 10 5

  C． 2 5

  D． 2 5
  组卷：76引用：5难度：0.8

  解析

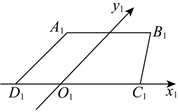• 4．如图，梯形A₁B₁C₁D₁是一水平放置的平面图形ABCD在斜二测画法下的直观图．若A₁D₁平行于y₁轴，

  A

  1

  B

  1

  ∥

  C

  1

  D

  1

  ，

  A

  1

  B

  1

  =

  3

  4

  C

  1

  D

  1

  =

  3

  ，

  A

  1

  D

  1

  =

  1

  ，则平面图形ABCD的面积是（　　）

  A．14

  B．7

  C． 7 2

  D． 14 2
  组卷：67引用：3难度：0.7

  解析

• 5．已知sinθ-5cosθ=0，则

  co

  s

  4

  θ

  -

  si

  n

  4

  θ

  si

  n

  2

  θ

  -

  sin

  2

  θ

  =（　　）

  A． - 8 5

  B． 8 5

  C． - 8 3

  D． 8 3
  组卷：204引用：2难度：0.7

  解析

• 6．在平行四边形ABCD中，对角线AC与BD交于点O，E为CD中点，AE与BD交于点F，若

  FE

  =

  1

  4

  AC

  +

  m

  BD

  ，则m=（　　）

  A． 1 4

  B． 3 4

  C． 1 12

  D． 1 6
  组卷：70引用：2难度：0.7

  解析

• 7．已知

  α

  ∈

  （

  π

  4

  ，

  π

  2

  ）

  ，a=（sinα）^sinα，b=（sinα）^tanα，c=（tanα）^sinα，则a,b,c的大小关系是（　　）

  A．a＜b＜c

  B．b＜a＜c

  C．b＜c＜a

  D．c＜a＜b
  组卷：66引用：2难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤.

• 21．已知向量

  a

  =

  （

  cosωx

  ,

  1

  ）

  ，

  b

  =

  （

  -

  3

  sinωx

  ,

  1

  ）

  （

  ω

  ＞

  0

  ）

  ，

  f

  （

  x

  ）

  =

  2

  a

  •

  （

  a

  -

  b

  ）

  -

  2

  ，且f（x）的最小正周期为π．
  （1）求f（x）在[0，π]上的单调递增区间；
  （2）将f（x）的图象上的点的纵坐标不变，横坐标伸长为原来的4倍，再把整个图象向左平移

  2

  3

  π

  个单位得到g（x）的图象，已知A（-2，2），B（2，5），则在g（x）上是否存在一点Q，使得

  QA

  ⊥

  QB

  ，若存在，求出Q的坐标，若不存在，说明理由．
  组卷：73引用：4难度：0.4

  解析

• 22．在△ABC中，内角A，B，C所对的边分别为a,b,c,AD⊥BC，垂足为D（D在边BC上且异于端点），设AD=h,且满足b+c=a+h.
  （1）若

  h

  =

  1

  2

  a

  ，求

  tan

  A

  2

  的值；
  （2）求

  tan

  A

  2

  的最小值．
  组卷：227引用：2难度：0.3

  解析