当前位置：试卷中心 > 试卷详情

2023-2024学年重庆市北碚区西南大学附中九年级（上）开学数学试卷

发布：2024/7/28 8:0:9

一.选择题（共10小题，满分40分，每小题4分）

1．下列各图是选自历届世界大运会的会徽图案，其中是轴对称图形的是（　　）
A． B． C． D．
组卷：82引用：2难度：0.9
解析
2．如图，△ABC与△DEF位似，点O为位似中心．已知OA：OD=1：3，且△ABC的周长为4，则△DEF的周长为（　　）
A．8 B．12 C．16 D．36
组卷：152引用：4难度：0.7
解析
3．对于二次函数y=3（x+4）²，其图象的顶点坐标为（　　）
A．（0，4） B．（0，-4） C．（4，0） D．（-4，0）
组卷：86引用：10难度：0.6
解析
4．估计
32
-
4
÷2的运算结果在哪两个整数之间（　　）
A．3和4 B．4和5 C．5和6 D．6和7
组卷：137引用：3难度：0.7
解析
5．如图，是由一些小棒搭成的图案，按照这种方式摆下去，摆第9个图案所用小棒的数量为（　　）
A．33 B．36 C．37 D．41
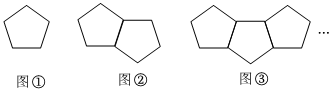组卷：303引用：8难度：0.6
解析
6．我市某家快递公司，今年8月份与10月份完成投递的快递总件数分别为2万件和2.88万件．若设该快递公司由8月份到10月份投递总件数的月平均增长率为x,则以下所列方程正确的是（　　）
A．2（1+x）=2.88
B．2（1+2x）=2.88
C．2（1+x）²=2.88
D．2+2（1+x）+2（1+x）²=2.88
组卷：299引用：4难度：0.5
解析
7．如图，在△ABC中，∠ABC=60°，∠C=45°，AD⊥BC，垂足为D，∠ABC的平分线交AD于点E，若
AE
=
6
，则AC的长为（　　）
A．
2
3
B．
3
3
2
C．
3
3
D．
3
6
2
组卷：77引用：3难度：0.5
解析
8．二次函数y=ax²+bx+c（a≠0）的图象的一部分如图所示．已知图象经过点（-1，0），其对称轴为直线x=1．下列结论：①abc＜0；②8a+c＜0；③a+b≥am²+bm；④不等式ax²+bx+c＞0的解集是-1＜x＜3；⑤若抛物线经过点（-3，n），则关于x的一元二次方程ax²+bx+c-n=0（a≠0）的两根分别为x₁=4、x₁=-3．上述结论中正确结论的个数为（　　）
A．1个 B．2个 C．3个 D．4个
组卷：613引用：5难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三.解答题（共8小题，满分78分）

25．如图，在平面直角坐标系中，抛物线
y
=
2
3
x
2
+
4
3
x
-
2
与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．
（1）求线段AC的长度；
（2）点P为直线AC下方抛物线上的一动点，且点P在抛物线对称轴左侧，过点P作PD∥y轴，交AC于点D，作PE∥x轴，交抛物线于点E．求3PD+PE的最大值及此时点P的坐标；
（3）在（2）中3PD+PE取得最大值的条件下，将该抛物线沿着射线CA方向平移
13
个单位长度，得到一条新抛物线y′，M为射线CA上的动点，过点M作MF∥x轴交新抛物线y′的对称轴于点F，点N为直角坐标系内一点，请直接写出所有使得以点P，F，M，N为顶点的四边形是菱形的点N的坐标，并写出求解点N的坐标的其中一种情况的过程．

组卷：810引用：5难度：0.1
解析
26．在△ABC中，90°＜∠BAC＜120°，将线段AB绕点A逆时针旋转120°得到线段AD，连接CD．
（1）如图1，若AB=8，∠ABC=45°，BA⊥CD，延长BA，CD交于点K，求四边形ABCD的面积；
（2）如图2，点E是CA延长线上一点，点G是AE的中点，连接BE，BG，点F在线段AC上，点H在线段BG上，连接HF，若BG=GF，HF=BE，GA=GH，2∠ACB=∠EBG+∠ABC，求证：BC+CD=
3
AC；
（3）如图3，在（1）的条件下，点P是线段BC上的一个动点，连接DP，将线段DP绕点D逆时针旋转45°得到线段DP'，连接AP'，BP'，点M是△ABP'内任意一点，点P在运动过程中，AM+BM+P'M是否存在最小值；若存在，请直接写出：AM+BM+P'M的最小值；若不存在，请说明理由．
组卷：664引用：3难度：0.1
解析