2022-2023学年广东省江门市高二(上)调研数学试卷(一)
发布:2024/7/12 8:0:9
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知数列{an}满足a1=2,
,则该数列的第5项为( )an=2-1an-1(n≥2且n∈N+)组卷:38引用:3难度:0.7 -
2.已知A(4,9),B(6,3)两点,以线段AB为直径的圆的标准方程是( )
组卷:86引用:5难度:0.7 -
3.直线
的倾斜角及在y轴上的截距分别是( )3x+y+2=0组卷:22引用:3难度:0.7 -
4.若
构成空间的一个基底,则下列向量不共面的是( ){a,b,c}组卷:49引用:2难度:0.5 -
5.已知M是抛物线y2=16x上的一点且在x轴上方,F是抛物线的焦点,以Fx为始边,FM为终边的角∠xFM=60°,则|FM|等于( )
组卷:7引用:3难度:0.6 -
6.直线Ax+By+C=0(A,B不同时为0),则下列选项正确的是( )
组卷:14引用:3难度:0.8 -
7.已知{an}为等差数列,a1+a3+a5=45,a2+a4+a6=33,则S10等于( )
组卷:10引用:2难度:0.7
四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
-
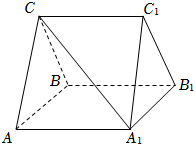 21.如图,在三棱柱ABC-A1B1C1中,平面ABC⊥平面AA1B1B,AC=BC,四边形AA1B1B是边长为2的菱形,∠BAA1=60°.
21.如图,在三棱柱ABC-A1B1C1中,平面ABC⊥平面AA1B1B,AC=BC,四边形AA1B1B是边长为2的菱形,∠BAA1=60°.
(1)证明:AB⊥A1C;
(2)若点B1到平面ACA1的距离为,求平面BA1A和平面CA1A夹角的余弦值.263组卷:125引用:5难度:0.5 -
22.已知平面上的动点P(x,y)总满足关系式
.(x+3)2+y2+(x-3)2+y2=4
(1)判断点P的轨迹是什么曲线?并求其轨迹E方程;
(2)设不经过点B(0,1)的直线l与曲线E相交于不同的两点M,N,若点B在以线段MN为直径的圆上,证明:直线l经过定点,并求出该定点的坐标.组卷:3引用:2难度:0.5


