2023-2024学年湖南省郴州市宜章一中高二（上）半月考数学试卷（9月份）

一、单项选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知复数z在复平面内对应的点是（0，1），则

  1

  +

  i

  z

  =（　　）

  A．1+i

  B．1-i

  C．-1+i

  D．-1-i
  组卷：64引用：6难度：0.8

  解析

• 2．在正方体ABCD-A₁B₁C₁D₁中，可以作为空间向量的一组基底的是（　　）

  A． AB ， AC ， AD	B． AB ， A A 1 ， A B 1
  C． D 1 A 1 ， D 1 C 1 ， D 1 D	D． A C 1 ， A 1 C ， C C 1
  组卷：53引用：4难度：0.7

  解析

• 3．“m=2”是“直线2x+（m+1）y+4=0与直线3x-my-2=0垂直”的（　　）

  A．充分必要条件	B．充分不必要条件
  C．必要不充分条件	D．既不充分也不必要条件
  组卷：223引用：7难度：0.8

  解析

• 4．在平面直角坐标系xOy中，点（0，4）关于直线x-y+1=0的对称点为（　　）

  A．（-1，2）

  B．（2，-1）

  C．（1，3）

  D．（3，1）
  组卷：612引用：4难度：0.7

  解析

• 5．方程

  （

  3

  x

  -

  y

  +

  1

  ）

  （

  y

  -

  1

  -

  x

  2

  ）

  =

  0

  表示的曲线为（　　）

  A．两条线段	B．一条线段和一个圆
  C．一条线段和半个圆	D．一条射线和半个圆
  组卷：85引用：1难度：0.5

  解析

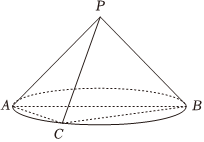• 6．轴截面为等腰直角三角形的圆锥为直角圆锥，如图所示，在直角圆锥P-ABC中，AB为底面圆的直径，C在底面圆周上且为弧

  ˆ

  AB

  的中点，则异面直线PB与AC所成角的大小为（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：134引用：4难度：0.7

  解析

• 7．已知函数

  f

  （

  x

  ）

  =

  cos

  （

  ωx

  +

  φ

  ）

  （

  ω

  ＞

  0

  ，

  |

  φ

  |

  ＜

  π

  2

  ）

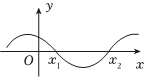  的部分图象如图所示，x₁，x₂是f（x）的两个零点，若x₂=4x₁，则下列为定值的量是（　　）

  A．φ

  B．ω

  C． φ ω

  D．ω+φ
  组卷：143引用：4难度：0.7

  解析

四、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤）

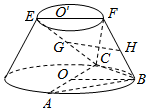• 21．在如图所示的圆台中，AC是下底面圆O的直径，EF是上底面圆O'的直径，FB是圆台的一条母线．
  （Ⅰ）已知G，H分别为EC，FB的中点，求证：GH∥平面ABC；
  （Ⅱ）已知EF=FB=

  1

  2

  AC=2

  3

  ，AB=BC，求平面FBC与平面ABC的夹角的余弦值．
  组卷：108引用：2难度：0.5

  解析

• 22．对于函数f（x），若在定义域内存在实数x₀，满足f（-x₀）=-f（x₀），则称f（x）为“M类函数”．
  （1）已知函数

  f

  （

  x

  ）

  =

  2

  cos

  （

  x

  -

  π

  3

  ）

  ，试判断f（x）是否为“M类函数”？并说明理由；
  （2）设f（x）=4^x-m•2^x+1-3是定义域R上的“M类函数”，求实数m的取值范围；
  （3）若

  f

  （

  x

  ）

  =

  lo g 2 （ x 2 - 2 mx ） ， x ＞ 3

  - 2 ， x ＜ 3

  为其定义域上的“M类函数”，求实数m取值范围．
  组卷：38引用：2难度：0.4

  解析