2022-2023学年云南省部分名校高一（上）期中数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．命题“∀x＜1，x²-x≤2”的否定是（　　）

  A．∀x＜1，x2-x＞2	B．∃x＜1，x2-x＞2
  C．∃x＜1，x2-x≥2	D．∃x≥1，x2-x＞2
  组卷：18引用：4难度：0.7

  解析

• 2．若全集U={-1，0，1，2，3，5}，集合A满足∁_UA={0，1，2}，则A=（　　）

  A．{-1}

  B．{-1，1}

  C．{-1，3，5}

  D．{-1，0，5}
  组卷：41引用：6难度：0.9

  解析

• 3．若函数f（x）的定义域为[0，2]，值域为[0，2]，则f（x）的图象可能为（　　）

  A．

  B．

  C．

  D．
  组卷：14引用：5难度：0.8

  解析

• 4．已知函数f（x）=x³-x+7，若f（-a）=1，则f（a）=（　　）

  A．-1

  B．6

  C．8

  D．13
  组卷：139引用：4难度：0.7

  解析

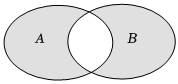• 5．定义：差集M-N={x|x∈M且x∉N}．现有两个集合A、B，则阴影部分表示的集合是（　　）

  A．（A-B）∪B	B．（B-A）∩B
  C．（A-B）∩（B-A）	D．（A-B）∪（B-A）
  组卷：82引用：6难度：0.7

  解析

• 6．若函数f（x³-1）=x²-|x|+2，则f（7）=（　　）

  A．44

  B．8

  C．4

  D．2
  组卷：1引用：2难度：0.7

  解析

• 7．函数

  f

  （

  x

  ）

  =

  8

  -

  x

  2

  2

  x

  3

  的大致图象是（　　）

  A．

  B．

  C．

  D．
  组卷：8引用：2难度：0.7

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．已知f（x）是定义域为R的奇函数，当x＜0时，

  f

  （

  x

  ）

  =

  2

  -

  3

  x

  3

  x

  3

  -

  1

  ．
  （1）求f（x）的解析式；
  （2）判断f（x）在（0，+∞）上的单调性，并用定义证明．
  组卷：23引用：3难度：0.6

  解析

• 22．已知函数f（x）=-x²+4|x-a|+2a.
  （1）若a=0，求f（x）的最大值；
  （2）若f（x）的最大值为g（a），求g（a）的最小值．
  组卷：17引用：2难度：0.5

  解析