2022-2023学年广东省广州市天河区华南师大附中七年级（上）月考数学试卷（10月份）

一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的.

• 1．今年是全民义务植树开展40周年．40年来，全民义务植树在中华大地蓬勃展开．截止12月13日，全国适龄公民累计17500000000人次参加义务植树，累计植树78100000000株（含折算），数据“17500000000”用科学记数法表示为（　　）

  A．1.75×108

  B．17.5×108

  C．1.75×109

  D．1.75×1010
  组卷：39引用：6难度：0.8

  解析

• 2．下列说法正确的是（　　）

  A．-1的相反数是1	B．-1的倒数是1
  C．-1的绝对值是±1	D．-1是最小的负整数
  组卷：166引用：2难度：0.9

  解析

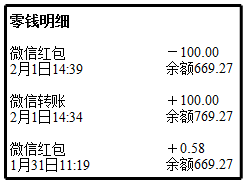• 3．如图所示的是某用户微信支付情况，-100表示的意思是（　　）

  A．发出100元红包	B．收入100元
  C．余额100元	D．抢到100元红包
  组卷：1635引用：34难度：0.9

  解析

• 4．下列说法中正确的是（　　）

  A．正分数和负分数统称为分数

  B．正整数、负整数统称为整数

  C．零既可以是正整数，也可以是负整数

  D．一个有理数不是正数就是负数
  组卷：3137引用：45难度：0.7

  解析

• 5．已知有理数a,b在数轴上表示的点如图所示，则下列结论中正确的是（　　）

  A．a-b＞0

  B．a+b＞0

  C． a b 小于-1

  D．ab＞0
  组卷：143引用：5难度：0.7

  解析

• 6．若（m-2）²与|n+3|互为相反数，则（m+n）²⁰²¹的值是（　　）

  A．-1

  B．1

  C．2021

  D．-2021
  组卷：583引用：5难度：0.6

  解析

• 7．计算1-2+3-4+5-6+7-8+…+2017-2018的结果是（　　）

  A．-1009

  B．-2018

  C．0

  D．-1
  组卷：90引用：4难度：0.6

  解析

• 8．若|a|=4，|b|=2，且a+b的绝对值与相反数相等，则a-b的值是（　　）

  A．-2

  B．-6

  C．-2或-6

  D．2或6
  组卷：557引用：11难度：0.7

  解析

三、解答题（本大题共8小题，共72分.请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）

• 23．概念学习
  规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如2÷2÷2，（-3）÷（-3）÷（-3）÷（-3）等，类比有理数的乘方，我们把2÷2÷2记作2₃，读作“2的3次商”，（-3）÷（-3）÷（-3）÷（-3）记作（-3）₄，读作“-3的4次商”．一般地，我们把n个a（a≠0）相除记作a_n，读作“a的n次商”．
  初步探究
  （1）直接写出结果：2₃=

  ；
  （2）关于除方，下列说法错误的是

  ；
  ①任何非零数的2次商都等于1；②对于任何正整数n,（-1）_n=-1；③3₄=4₃；④负数的奇数次商结果是负数，负数的偶数次商结果是正数．
  深入思考
  我们知道，有理数的减法运算可以转化为加法运算，除法运算能够转化为乘法运算，那么有理数的除方运算如何转化为乘方运算呢？例：

  2

  4

  =

  2

  ÷

  2

  ÷

  2

  ÷

  2

  =

  2

  ×

  1

  2

  ×

  1

  2

  ×

  1

  2

  =

  （

  1

  2

  ）

  2

  ．
  （3）试一试：仿照上面的算式，将下列运算结果直接写成乘方（幂）的形式（-3）₄=

  ；

  （

  1

  7

  ）

  5

  =

  ；
  （4）想一想：将一个非零有理数a的n次商写成幂的形式等于

  ；
  （5）算一算：

  5

  2

  ÷

  （

  -

  1

  2

  ）

  4

  ×

  （

  -

  1

  3

  ）

  5

  +

  （

  -

  1

  4

  ）

  3

  ×

  1

  4

  =

  ．
  组卷：389引用：16难度：0.6

  解析

• 24．在数学问题中，我们常用几何方法解决代数问题，借助数形结合的方法使复杂问题简单化．
  材料一：我们知道|a|的几何意义是：数轴上表示数a的点到原点的距离；|a-b|的几何意义是：数轴上表示数a,b的两点之间的距离；|a+b|的几何意义是：数轴上表示数a,-b的两点之间的距离；根据绝对值的几何意义，我们可以求出以下方程的解．
  （1）|x-3|=4
  解：由绝对值的几何意义知：
  在数轴上x表示的点到3的距离等于4
  ∴x₁=3+4=7，x₂=3-4=-1
  （2）|x+2|=5
  解：∵|x+2|=|x-（-2）|，∴其绝对值的几何意义为：在数轴上x表示的点到-2的距离等于5．∴x₁=-2+5=3，x₂=-2-5=-7
  材料二：如何求|x-1|+|x+2|的最小值．
  由|x-1|+|x+2|的几何意义是数轴上表示数x的点到表示数1和-2两点的距离的和，要使和最小，则表示数x的这点必在-2和1之间（包括这两个端点）取值．
  ∴|x-1|+|x+2|的最小值是3；由此可求解方程|x-1|+|x+2|=4，把数轴上表示x的点记为点P，由绝对值的几何意义知：当-2≤x≤1时，|x-1|+|x+2|恒有最小值3，所以要使|x-1|+|x+2|=4成立，则点P必在-2的左边或1的右边，且到表示数-2或1的点的距离均为0.5个单位．
  故方程|x-1|+|x+2|=4的解为：x₁=-2-0.5=-2.5，x₂=1+0.5=1.5．
  阅读以上材料，解决以下问题：
  （1）填空：|x-3|+|x+2|的最小值为

  ；
  （2）已知有理数x满足：|x+3|+|x-10|=15，有理数y使得|y-3|+|y+2|+|y-5|的值最小，求x-y的值．
  （3）试找到符合条件的x,使|x-1|+|x-2|+…+|x-n|的值最小，并求出此时的最小值及x的取值范围．
  组卷：923引用：4难度：0.6

  解析