2022-2023学年湖南省永州一中高一(下)月考数学试卷(6月份)
发布:2024/5/29 8:0:9
一、单选题
-
1.已知复数z1=3+4i,z2=3-4i,则z1+z2=( )
组卷:52引用:4难度:0.9 -
2.已知点G是三角形ABC所在平面内一点,满足
+GA+GB=GC,则G点是三角形ABC的( )0组卷:125引用:3难度:0.7 -
3.已知m,n表示两条不同的直线,α表示平面.下列说法正确的是( )
组卷:1204引用:16难度:0.6 -
4.在△ABC中,角A,B,C的对边分别为a,b,c.若
,则c的值为( )a=2,b=3,C=30°组卷:397引用:5难度:0.7 -
5.在△ABC中,若a=3,cosA=-
,则△ABC的外接圆半径是( )12组卷:175引用:6难度:0.9 -
6.已知正方形ABCD的边长为1,点P是对角线BD上任意一点,则
的取值范围为( )AP•BD组卷:659引用:5难度:0.5 -
7.1748年,瑞士数学家欧拉发现了复指数函数和三角函数的关系,并写出以下公式eix=cosx+isinx,其中e是自然对数的底,i是虚数单位,这个公式在复变论中占有非常重要的地位,被誉为“数学中的天桥”,下列说法正确的是( )
组卷:37引用:3难度:0.7
四、解答题
-
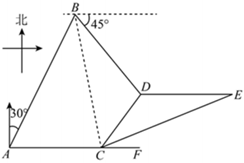 21.如图,某巡逻艇在A处发现北偏东30°相距海里的B处有一艘走私船,正沿东偏南45°的方向以3海里/小时的速度向我海岸行驶,巡逻艇立即以26+2海里/小时的速度沿着正东方向直线追去,1小时后,巡逻艇到达C处,走私船到达D处,此时走私船发现了巡逻艇,立即改变航向,以原速向正东方向逃窜,巡逻艇立即加速以32海里/小时的速度沿着直线追击.2
21.如图,某巡逻艇在A处发现北偏东30°相距海里的B处有一艘走私船,正沿东偏南45°的方向以3海里/小时的速度向我海岸行驶,巡逻艇立即以26+2海里/小时的速度沿着正东方向直线追去,1小时后,巡逻艇到达C处,走私船到达D处,此时走私船发现了巡逻艇,立即改变航向,以原速向正东方向逃窜,巡逻艇立即加速以32海里/小时的速度沿着直线追击.2
(1)当走私船发现了巡逻艇时,两船相距多少海里
(2)问巡逻艇应该沿什么方向去追,才能最快追上走私船.组卷:127引用:6难度:0.6 -
22.如图,在平行四边形ABCD中,∠ABC=60°,AD=2AB=4,E为AD的中点,以EC为折痕将△CDE折起,使点D到达点P的位置,且PB=
,F,G分别为BC,PE的中点.10
(1)证明:PB∥平面AFG;
(2)若平面PAB与平面PEF的交线为l,求直线l与平面PBC所成角的正弦值.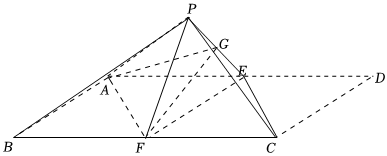 组卷:307引用:5难度:0.3
组卷:307引用:5难度:0.3


