2023-2024学年天津市南开中学高三（上）统练数学试卷（二）

一、选择题（每小题5分，共60分）

• 1．已知集合

  A

  =

  {

  x

  |

  y

  =

  1

  -

  4

  x

  2

  }

  ，B={x|ln（1-x）≤0}，则A∪B=（　　）

  A． [ - 1 2 ， + ∞ ）

  B． [ - 1 2 ， 1 ）

  C．[0，1）

  D．[0，1]
  组卷：87引用：2难度：0.7

  解析

• 2．“0＜a＜b”是“lg|a|-b²＜lg|b|-a²”的（　　）

  A．充分不必要条件	B．必要不充分条
  C．充要条件	D．既不充分也不必要条件
  组卷：270引用：7难度：0.7

  解析

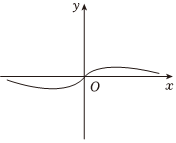• 3．已知函数f（x）=x,g（x）=2^x+2^-x，则大致图象如图的函数可能是（　　）

  A．f（x）+g（x）

  B．f（x）-g（x）

  C．f（x）g（x）

  D． f （ x ） g （ x ）
  组卷：311引用：6难度：0.7

  解析

• 4．设a=2020^0.7，b=2021^0.8，c=log₂₀₂₃2022，则a,b,c的大小关系为（　　）

  A．a＜b＜c

  B．b＜a＜c

  C．b＜c＜a

  D．c＜a＜b
  组卷：191引用：5难度：0.8

  解析

• 5．当0＜x≤

  1

  2

  时，4^x＜log_ax,则实数a的取值范围是（　　）

  A．（1，2）

  B．（2，+∞）

  C． （ 0 ， 2 2 ）

  D． （ 2 2 ， 1 ）
  组卷：109引用：2难度：0.9

  解析

• 6．对数的发明并非来源于指数，而是源于数学家对简化大数运算的有效工具的追求．其关键是利用对应关系q^k→k：[q⁰，q¹，q²，⋯，qⁿ，⋯]→[0，1，2，⋯，n,⋯]．观察下表：
  

  b	⋯	13	14	15	⋯	27	28	29	⋯
  N=2b	⋯	8192	16384	32768	⋯	134217728	268435456	536870912	⋯

  已知299792.468（km/s）是光在真空中的速度，31536000是一年的总秒数（假设一年365天），根据表中数据，计算M=log₂（299792.468×31536000），则M一定落在区间（　　）

  A．（40，42）

  B．（42，44）

  C．（44，46）

  D．（46，48）
  组卷：49引用：2难度：0.7

  解析

• 7．已知函数

  f

  （

  x

  ）

  =

  lo

  g

  1

  2

  （

  3

  x

  2

  -

  ax

  +

  8

  ）

  在[-1，+∞）上单调递减，则实数a的取值范围是（　　）

  A．（-∞，-6]

  B．[-11，-6]

  C．（-11，-6]

  D．（-11，+∞）
  组卷：382引用：3难度：0.7

  解析

三、解答题（共60分）

• 21．已知函数f（x）=alnx-x²+3x+3a.
  （Ⅰ）当a=2时，求f（x）的极值．
  （Ⅱ）讨论f（x）的单调性；
  （Ⅲ）若

  0

  ＜

  a

  ＜

  1

  4

  ，证明：

  f

  （

  x

  ）

  ＜

  e

  x

  x

  -

  x

  2

  +

  3

  x

  ．
  组卷：541引用：5难度：0.3

  解析

• 22．已知a＞0，函数f（x）=ax-xe^x．
  （1）求曲线f（x）在点（0，f（0））处的切线方程；
  （2）证明函数f（x）存在唯一的极值点；
  （3）若∃a,使得f（x）≤a+b对任意的x∈R恒成立，求实数b的取值范围．
  组卷：5213引用：5难度：0.5

  解析