2022-2023学年北京市顺义区高一（下）期末数学试卷

一、选择题共10小题，每小题4分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．

• 1．在平面直角坐标系中，A（-2，1），B（1，0），则向量

  AB

  =（　　）

  A．（-3，1）

  B．（3，-1）

  C．（-3，-1）

  D．（3，1）
  组卷：124引用：2难度：0.9

  解析

• 2．在以下4项调查中：
  ①调查一个40人班级的学生每周的体育锻炼时间；
  ②调查某省的一种结核病的发病率；
  ③调查一批食品的合格率；
  ④调查一个水库所有鱼中草鱼所占的比例；
  适合用全面调查的是（　　）

  A．①

  B．②

  C．③

  D．④
  组卷：159引用：1难度：0.8

  解析

• 3．复数z=i（2+i）在复平面内对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：73引用：2难度：0.8

  解析

• 4．已知向量

  a

  =

  （

  m

  ,

  2

  ）

  ，

  b

  =

  （

  -

  2

  ，

  1

  ）

  ，若

  a

  ⊥

  b

  ，则实数m=（　　）

  A．-4

  B．-1

  C．1

  D．4
  组卷：101引用：1难度：0.9

  解析

• 5．某中学高一年级有280人，高二年级有320人，为了解该校高一高二学生对暑假生活的规划情况，现用比例分配的分层随机抽样方法抽取一个容量为60的样本，则高一年级应抽取的人数为（　　）

  A．14

  B．16

  C．28

  D．32
  组卷：142引用：3难度：0.9

  解析

• 6．若α，β是两个不同的平面，则“存在两条异面直线m,n,满足m∥β，n∥α”是“α∥β”的（　　）

  A．充分而不必要条件	B．必要而不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：103引用：1难度：0.5

  解析

• 7．为了得到函数

  y

  =

  cos

  （

  π

  4

  -

  x

  ）

  的图象，只需把函数y=sinx的图象（　　）

  A．向左平移 π 4 个单位长度	B．向右平移 π 4 个单位长度
  C．向左平移 π 2 个单位长度	D．向右平移 π 2 个单位长度
  组卷：178引用：1难度：0.8

  解析

三、解答题共6道题，共85分，解答应写出文字说明，证明过程或演算步骤．

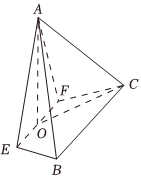• 20．如图，在四棱锥A-EFCB中，△AEF为等边三角形，平面AEF⊥平面EFCB，EF∥BC，BC=2，EF=a,∠EBC=∠FCB=60°，O为EF的中点．
  （Ⅰ）求证：BC∥平面AEF；
  （Ⅱ）求证：AO⊥BE；
  （Ⅲ）若BE⊥平面AOC，求实数a的值．
  组卷：304引用：1难度：0.8

  解析

• 21．设集合A为n元数集，若A的2个非空子集B，C满足：B∪C=A，B∩C=∅，则称B，C为A的一个二阶划分．记B中所有元素之和为S（B），C中所有元素之和为S（C）．
  （Ⅰ）若A={1，2，3}，求A的一个二阶划分，使得S（B）=2S（C）；
  （Ⅱ）若A={1，2，⋯，10}．求证：不存在A的二阶划分B，C满足S（C）=2S（B）；
  （Ⅲ）若A={1，2，⋯，n}（n≥3，n∈N^*），B，C为A的一个二阶划分，满足：①若x∈B，则2x∉B；②若x∈C，则2x∉C．
  记f（n）为符合条件的B的个数，求f（n）的解析式．
  组卷：155引用：3难度：0.5

  解析