2022-2023学年福建省厦门市双十中学高一(下)第二次月考数学试卷
发布:2024/6/24 8:0:9
一、单项选择题(本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的).
-
1.已知复数
为纯虚数,则实数a等于( )a+i1+i组卷:94引用:3难度:0.8 -
2.已知A(1,0),B(2,1),C(4,3),则( )
组卷:342引用:4难度:0.7 -
3.在△ABC中,已知a=
,b=2,B=60°,则角A等于( )3组卷:272引用:10难度:0.9 -
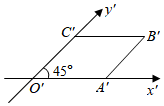 4.一个侧棱长为2的直棱柱的底面用斜二测画法所画出的水平放置的直观图为如图所示的菱形O′A′B′C′,其中O′A′=2,则该直棱柱的体积为( )3组卷:93引用:5难度:0.7
4.一个侧棱长为2的直棱柱的底面用斜二测画法所画出的水平放置的直观图为如图所示的菱形O′A′B′C′,其中O′A′=2,则该直棱柱的体积为( )3组卷:93引用:5难度:0.7 -
5.某公司2021年5月至2022年3月的各月利润率与每百元营业收入中的成本如图所示,则下列说法中正确的是( )
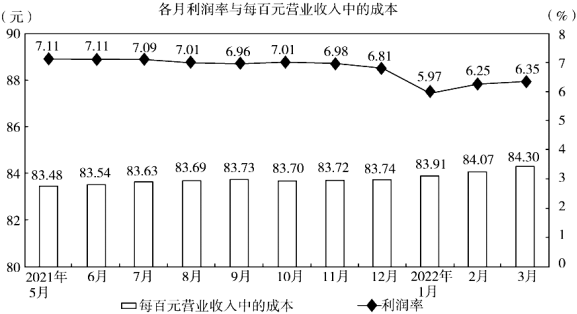 组卷:6引用:3难度:0.6
组卷:6引用:3难度:0.6 -
6.我国古代为了进行复杂的计算,曾经使用“算筹”表示数,后渐渐发展为算盘.算筹有纵式和横式两种排列方式,0~9各个数字及其算筹表示的对应关系如表:
排列数字时,个位采用纵式,十位采用横式,百位采用纵式,千位采用横式…纵式和横式依次交替出现.如“0 1 2 3 4 5 6 7 8 9 纵式 
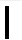
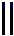







横式 





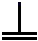
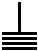

 ”表示21,“
”表示21,“ ”表示609.在由“
”表示609.在由“ ”、“
”、“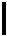 ”、“
”、“ ”、“
”、“ ”、“
”、“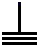 ”按照一定顺序排列成的三位数中任取一个,取到偶数的概率是( )组卷:16引用:4难度:0.8
”按照一定顺序排列成的三位数中任取一个,取到偶数的概率是( )组卷:16引用:4难度:0.8 -
7.已知一组数据x1,x2,…,xn(n≥2)的平均数为
,标准差为s,x,若M=1nn∑i=1(xi-a)2,则s与a≠x的大小关系为( )M组卷:92引用:2难度:0.7
四、解答题:共070分.解答应写出文字说明、证明过程或演算步骤.
-
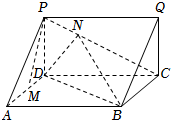 21.如图,在三棱柱ADP-BCQ中,侧面ABCD为矩形.
21.如图,在三棱柱ADP-BCQ中,侧面ABCD为矩形.
(1)设M为AD中点,点N在线段PC上且NC=2PN,求证:PM∥平面BDN;
(2)若二面角Q-BC-D的大小为θ,,且AD=|cosθ|AB,求直线BD和平面QCB所成角的正弦值的取值范围.θ∈[π4,5π6]组卷:136引用:3难度:0.6 -
22.已知正△ABC的边长为
,内切圆圆心为I,点P满足43.|PI|=1
(1)求证:为定值;PA2+PB2+PC2
(2)把三个实数a,b,c的最小值记为min{a,b,c},若m=min{•PA,PB•PB,PC•PA},求m的取值范围;PC
(3)若(x,y,z∈R+),求当xPA+yPB+zPC=0取最大值时,xy的值.zx+y组卷:101引用:4难度:0.6


