2023年陕西省西安市碑林区尊德中学中考数学五模试卷

一、选择题（本题共8小题，每题3分，共24分）

• 1．

  1

  5

  的倒数是（　　）

  A．-5

  B．5

  C．- 1 5

  D． 1 5
  组卷：311引用：8难度：0.7

  解析

• 2．下列运算正确的是（　　）

  A．（-3a）2=6a2	B．（a2）2=a5
  C．a2•a3=a6	D．（-a）3÷（-a）=a2
  组卷：281引用：5难度：0.9

  解析

• 3．已知点（3，-1）是双曲线

  y

  =

  k

  x

  （

  k

  ≠

  0

  ）

  上一点，则下列各点不在该图象上的点是（　　）

  A． （ 1 2 ，- 6 ）

  B．（-1，-3）

  C．（-1，3）

  D． （ - 9 ， 1 3 ）
  组卷：172引用：3难度：0.5

  解析

• 4．如图，AB∥CD，EF⊥AB于点E，EF交CD于点F，EM交CD于点M，已知∠1=57°，则∠2的度数为（　　）

  A．33°

  B．57°

  C．43°

  D．123°
  组卷：322引用：8难度：0.6

  解析

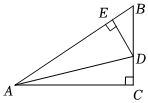• 5．如图，在Rt△ABC中，∠C=90°，点D和点E分别是BC和AB上的点，已知DE⊥AB，

  sin

  B

  =

  4

  5

  ，AC=8，CD=2，则DE的长为（　　）

  A．3.2

  B．4

  C．4.5

  D．4.8
  组卷：577引用：8难度：0.7

  解析

• 6．已知平行四边形ABCD的对角线相交于点O，补充下列四个条件，能使平行四边形ABCD成为菱形的是（　　）

  A．AB=BD

  B．AC=BD

  C．∠DAB=90°

  D．∠AOB=90°
  组卷：1343引用：11难度：0.5

  解析

• 7．如图，在△ABC中，AB=AC，三个顶点A，B，C均在⊙O上，BD过圆心O，连接AD．当∠OBC=40°时，∠ADB的度数是（　　）

  A．45°

  B．55°

  C．65°

  D．75°
  组卷：292引用：4难度：0.6

  解析

• 8．将抛物线y=-x²+2x-3先向左平移2个单位长度，再向上平移6个单位长度，平移后的抛物线与x轴交于A、B两点，顶点是C点，连接AC、BC，则sin∠CAB的值为（　　）

  A． 5 4

  B． 2 5 5

  C． 4 5

  D． 5 2
  组卷：580引用：5难度：0.5

  解析

三、解答题（共13题，计81分，解答应写出过程）

• 25．如图，已知抛物线y=-x²+2x+c与x轴交于点A（3，0），B，与y轴交于点C．
  （1）求c的值及该抛物线的对称轴；
  （2）若点D在直线AC上，点E是平面内一点．是否存在点E，使得以点A，B，D，E为顶点的四边形为正方形？若存在，请求出点E的坐标；若不存在，请说明理由．
  组卷：496引用：2难度：0.4

  解析

• 26．问题提出
  （1）如图，AB是⊙O的弦，点C是⊙O上的一点，在直线AB上方找一点D，使得∠ADB=∠ACB，画出∠ADB，并说明理由；
  问题探究
  （2）如图，AB是⊙O的弦，直线l与⊙O相切于点M，点M，是直线l上异于点M的任意一点，请在图中画出图形，试判断∠AMB，∠AM₁B的大小关系；并说明理由；
  问题解决
  （3）如图，有一个平面图为五边形ABCDE的展览馆，其中AE=DE=40m,AB=CD=30m,∠A=∠E=∠D=90°．展览馆保卫人员想在线段DE上选一点M安装监控装置，用来监视边BC，现只要使∠BMC最大，就可以让监控装置的效果达到最佳，问在线段DE上是否存在点M，使∠BMC最大？若存在，请求出符合条件的DM的长，若不存在，请说明理由．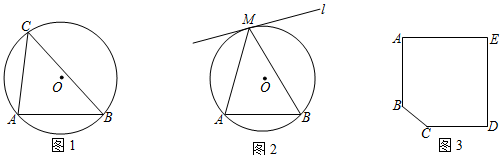
  
  组卷：325引用：2难度：0.1

  解析