2022-2023学年广东省实验中学附属江门学校高二（上）开学数学试卷

一、单选题（本大题共8小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）

• 1．已知向量

  a

  =（2，3），

  b

  =（3，2），则|

  a

  -

  b

  |=（　　）

  A． 2

  B．2

  C．5 2

  D．50
  组卷：8079引用：46难度：0.8

  解析

• 2．设

  e

  1

  ，

  e

  2

  为平面内一个基底，已知向量

  AB

  =

  e

  1

  -

  k

  e

  2

  ，

  CB

  =

  4

  e

  1

  -

  2

  e

  2

  ，

  CD

  =

  3

  e

  1

  -

  3

  e

  2

  ，若A，B，D三点共线，则k的值是（　　）

  A．2

  B．1

  C．-2

  D．-1
  组卷：228引用：6难度：0.6

  解析

• 3．在△ABC中，AD为BC边上的中线，E为AD的中点，则

  EB

  =（　　）

  A． 3 4 AB - 1 4 AC

  B． 1 4 AB - 3 4 AC

  C． 3 4 AB + 1 4 AC

  D． 1 4 AB + 3 4 AC
  组卷：17509引用：166难度：0.9

  解析

• 4．南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库．已知该水库水位为海拔148.5m时，相应水面的面积为140.0km²；水位为海拔157.5m时，相应水面的面积为180.0km²．将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148.5m上升到157.5m时，增加的水量约为（

  7

  ≈2.65）（　　）

  A．1.0×109m3

  B．1.2×109m3

  C．1.4×109m3

  D．1.6×109m3
  组卷：4030引用：20难度：0.7

  解析

• 5．设m,n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是（　　）

  A．若α⊥β，m⊂α，n⊂β，则m⊥n	B．若m⊥α，m∥n,n∥β，则α⊥β
  C．若m⊥n,m⊂α，n⊂β，则α⊥β	D．若α∥β，m⊂α，n⊂β，则m∥n
  组卷：1505引用：163难度：0.9

  解析

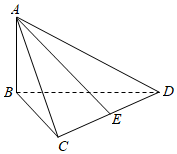• 6．如图，三棱锥A-BCD中，AB⊥底面BCD，BC⊥CD，且AB=BC=1，CD=2，点E为CD的中点，则AE的长为（　　）

  A． 2

  B． 3

  C．2

  D． 5
  组卷：197引用：5难度：0.7

  解析

• 7．刘徽（约公元225年-295年），魏晋时期伟大的数学家，中国古代数学理论的奠基人之一．他在割圆术中提出的“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”，这可视为中国古代极限观念的重要阐释．割圆术的核心思想是将一个圆的内接正n边形等分成n个等腰三角形，当n变得很大时，这些等腰三角形的面积之和近似等于圆的面积．运用割圆术的思想，得到sin1°的近似值为（　　）

  A． π 90

  B． π 180

  C． π 270

  D． π 360
  组卷：208引用：4难度：0.7

  解析

四、解答题（本大题共6小题，其中18题10分，其余每题12分，共70.0分。解答应写出文字说明，证明过程或演算步骤）

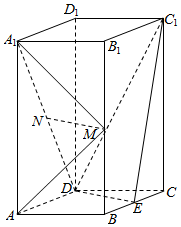• 21．如图，直四棱柱ABCD-A₁B₁C₁D₁的底面是菱形，AA₁=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB₁，A₁D的中点．
  （1）证明：MN∥平面C₁DE；
  （2）求点C到平面C₁DE的距离．
  组卷：7595引用：34难度：0.4

  解析

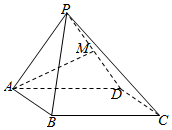• 22．如图，在四棱锥P-ABCD中，底面ABCD为正方形，侧面PAD是正三角形，侧面PAD⊥底面ABCD，M是PD的中点．
  （1）求证：AM⊥平面PCD；
  （2）求侧面PBC与底面ABCD所成二面角的余弦值．
  组卷：962引用：17难度：0.5

  解析