刘徽（约公元225年-295年），魏晋时期伟大的数学家，中国古代数学理论的奠基人之一．他在割圆术中提出的“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”，这可视为中国古代极限观念的重要阐释．割圆术的核心思想是将一个圆的内接正n边形等分成n个等腰三角形，当n变得很大时，这些等腰三角形的面积之和近似等于圆的面积．运用割圆术的思想，得到sin1°的近似值为（ ）
【考点】扇形面积公式．
【答案】B
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/1 8:0:9组卷：208引用：4难度：0.7
相似题
-
1．已知扇形的半径为1，圆心角为30°，则扇形的面积为（ ）
发布：2024/12/29 13:0:1组卷：378引用：7难度：0.7 -
2．密位制是度量角的一种方法．把一周角等分为6000份，每一份叫做1密位的角．以密位作为角的度量单位，这种度量角的单位制，叫做角的密位制．在角的密位制中，采用四个数码表示角的大小，单位名称密位二字可以省去不写．密位的写法是在百位数与十位数字之间画一条短线，如密位7写成“0-07”，478密位写成“4-78”，1周角等于6000密位，记作1周角=60-00，1直角=15-00．如果一个半径为2的扇形，它的面积为
，则其圆心角用密位制表示为（ ）75π发布：2025/1/2 23:30:3组卷：137引用：1难度：0.8 -
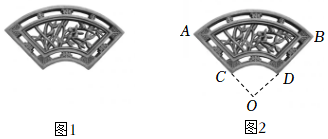3．扇子最早称“翣”，其功能并不是纳凉，而是礼仪器具，后用于纳凉、娱乐、欣赏等．扇文化是中国传统文化的重要门类，扇子的美学也随之融入到建筑等艺术审美之中．图1为一古代扇形窗子，此窗子所在扇形的半径（图2）AO=120cm,圆心角为45°，且C为AO的中点，则该扇形窗子的面积为（ ）发布：2024/12/29 13:0:1组卷：233引用：4难度：0.8
