2022-2023学年上海市浦东新区育民中学九年级（上）期中数学试卷

一、选择题：（本大题共6题，每题4分，满分24分）

• 1．已知线段b是线段a、c的比例中项，如果a=4，c=9，那么线段b的长为（　　）

  A． 9 4

  B．6

  C．±6

  D．36
  组卷：32引用：2难度：0.5

  解析

• 2．如果把一个三角形的三边的长扩大为原来的100倍，那么这个三角形的面积扩大为原来的（　　）

  A．10倍

  B．50倍

  C．200倍

  D．10000倍
  组卷：31引用：2难度：0.5

  解析

• 3．在Rt△ABC中，∠C=90°，若AC=6，BC=8，那么下列等式中正确的是（　　）

  A． sin A = 4 5

  B． tan A = 3 4

  C． cot A = 4 3

  D． cos B = 3 5
  组卷：48引用：2难度：0.5

  解析

• 4．在△ABC中，点D、E分别在△ABC的边AB、AC上，下列条件中能判定DE∥BC的是（　　）

  A． AD DB = AE AC

  B． DE BC = AE AC

  C． AD DB = EC AE

  D． DB AB = EC AC
  组卷：7引用：2难度：0.5

  解析

• 5．下列说法中不正确的是（　　）

  A． 0 a = 0

  B．对于非零向量 a 、 b 、 c ， a = - 1 2 c ， b = 2 c ，则 a ∥ b

  C．若 | a | = | b | ，那么 a = b 或 a = - b

  D．若 a 、 b 均为单位向量，那么 | a | = | b |
  组卷：48引用：2难度：0.5

  解析

• 6．依据下列条件不能判定△ABC和△DEF相似的是（　　）

  A．∠A=35°，∠B=∠E=65°，∠F=80°

  B．∠A=35°，AB=4cm,AC=6cm,∠D=35°，ED=8cm,EF=12cm

  C．AB=4cm,BC=5cm,CA=6cm,DE=8cm,EF=10cm,FD=12cm

  D．∠C=∠F=90°，AB=10cm,AC=8cm,DE=15cm,EF=9cm
  组卷：41引用：2难度：0.5

  解析

二、填空题：（本大题共12题，每题4分，满分48分）

• 7．已知2x=5y（y≠0），则

  x

  y

  =

  ．
  组卷：162引用：7难度：0.9

  解析

• 8．已知线段AB的长为4厘米，点P是线段AB的黄金分割点（AP＜BP），那么线段AP的长是

  厘米．
  组卷：147引用：2难度：0.6

  解析

三、解答题：（本大题共7题，共78分）

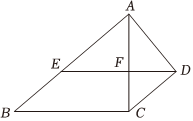• 24．如图，已知四边形ABCD中，过点D作DE∥BC、AB∥CD，分别交AB、AC于点E、F，且AB•AE=ED•BC．
  （1）求证：∠AFE=∠BAD；
  （2）求证：

  AE

  AB

  =

  D

  F

  2

  C

  D

  2

  ．
  组卷：55引用：2难度：0.5

  解析

• 25．在矩形ABCD中，AB=6，AD=8，点E是边BC上的一点，AE⊥EF交CD于点F，点G在射线CD上且满足EC²=CF⋅CG．
  
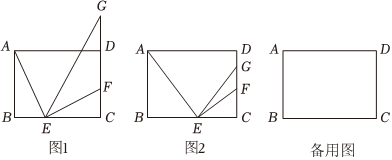
  （1）如图1，求证∠EGC=∠BAE；
  （2）如图2，当点G在线段CD上，连接AC，AC⊥EG，求GF的长；
  （3）连接AC，如果△AEC与以E、F、G为顶点所组成的三角形相似，求BE的长．
  组卷：73引用：2难度：0.2

  解析