在矩形ABCD中，AB=6，AD=8，点E是边BC上的一点，AE⊥EF交CD于点F，点G在射线CD上且满足EC2=CF⋅CG．
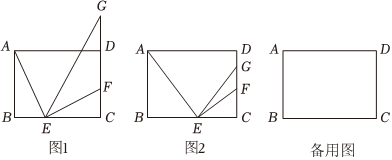
（1）如图1，求证∠EGC=∠BAE；
（2）如图2，当点G在线段CD上，连接AC，AC⊥EG，求GF的长；
（3）连接AC，如果△AEC与以E、F、G为顶点所组成的三角形相似，求BE的长．
【考点】相似形综合题．
【答案】（1）证明见解答过程；
（2）；
（3）或3．
（2）
49
24
（3）
BE
=
9
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/3 2:0:1组卷：73引用：2难度：0.2
相似题
-
1．图①、图②、图③都是5×4的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长为1，点A、B、C、D均在格点上．请按要求解答问题．（画图只能用无刻度的直尺，保留作图痕迹）
要求：（1）如图①，=；BECE
（2）如图②，在BC上找一点F使BF=2；
（3）如图③，在AC上找一点M，连结BM、DM，使△ABM∽△CDM．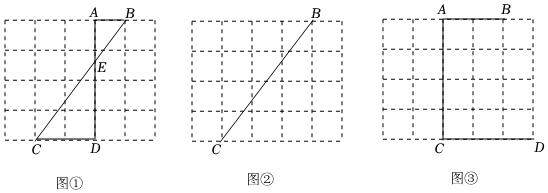
发布：2025/6/7 8:30:2组卷：210引用：4难度：0.5 -
2．小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．
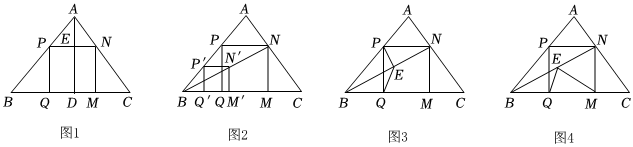
（1）温故：如图1，在△ABC中，AD⊥BC于点D，正方形PQMN的边QM在BC上，顶点P，N分别在AB，AC上，且．若BC=6，AD=4，则正方形PQMN的边长等于 ；PNBC+MNAD=1
（2）操作：能画出这类正方形吗？小波按数学家波利亚在《怎样解题》中的方法进行操作：如图2，任意画△ABC，在AB上任取一点P'，画正方形P'Q'M'N'，使Q'，M'在BC边上，N'在△ABC内，连结BN'并延长交AC于点N，画NM⊥BC于点M，NP⊥NM交AB于点P，PQ⊥BC于点Q，得到四边形PQMN；
（3）推理：如图3，若点E是BN的中点，求证：EP=EQ；
（4）拓展：在（2）的条件下，射线BN上截取NE=NM，连结EQ，EM（如图4）．当∠NBM=30°时，猜想∠QEM的度数，并尝试证明．
请帮助小波解决“温故”、“推理”、“拓展”中的问题．发布：2025/6/7 9:0:2组卷：103引用：3难度：0.3 -
3．如图①，在Rt△ABC中，∠C=90°，BC=8cm,AC=6cm,点P由A点出发以1cm/s的速度向终点C匀速移动，同时点Q由点C出发以2cm/s的速度向终点B匀速移动，当一个点到达终点时另一个点也随之停止移动．
（1）填空：在 秒时，△PCQ的面积为△ACB的面积的；38
（2）经过几秒，以P、C、Q为顶点的三角形与△ACB相似？
（3）如图②，D为AB上一点，且AD=AC，运动时间t为多少时，CD⊥PQ？发布：2025/6/9 4:30:2组卷：133引用：2难度：0.3
