当前位置：试卷中心 > 试卷详情

2022-2023学年山东省潍坊市高一（下）期末数学试卷

发布：2024/6/11 8:0:9

一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．已知复数
z
=
i
1
-
i
，则复数z的虚部为（　　）
A．
1
2
B．
-
1
2
C．
1
2
i
D．
-
1
2
i
组卷：109引用：3难度：0.9
解析
2．已知向量
a
=
（
1
，
3
）
，
b
=
（
3
，
λ
）
，若
a
⊥
b
，则实数λ的值为（　　）
A．7 B．3 C．-1 D．-3
组卷：52引用：3难度：0.9
解析
3．在平面直角坐标系xOy中，若角α的终边经过点M（-1，2），则
sin
（
π
2
+
α
）
=（　　）
A．
-
2
5
5
B．
-
5
5
C．
5
5
D．
2
5
5
组卷：151引用：2难度：0.8
解析
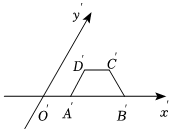4．已知水平放置的平面图形ABCD的直观图如图所示，其中A′B′∥D′C′，∠D′A′B′=45°，A′B′=3，C′D′=1，A′D′=1，则平面图形ABCD的面积为（　　）
A．6 B．3 C．8 D．4
组卷：117引用：5难度：0.8
解析
5．若
α
∈
（
0
，
π
2
）
，且
tan
2
α
=
cosα
2
-
sinα
，则sinα的值为（　　）
A．
15
4
B．
1
2
C．
1
3
D．
1
4
组卷：196引用：7难度：0.7
解析
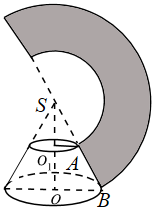6．如图，圆台OO₁的侧面展开图扇环的圆心角为180°，其中SA=2，SB=4，则该圆台的高为（　　）
A．1 B．
2
C．
3
D．4
组卷：120引用：3难度：0.8
解析
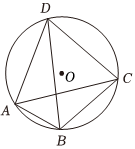7．托勒密是古希腊天文学家、地理学家，托勒密定理就是由其名字命名，该定理指出：圆的内接凸四边形两组对边乘积的和等于两条对角线的乘积．则图四边形ABCD为圆O的内接凸四边形，BD=6，BC=2AB，且△ACD为等边三角形，则圆O的直径为（　　）
A．
3
3
B．
21
3
C．
2
21
3
D．
4
21
3
组卷：70引用：1难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

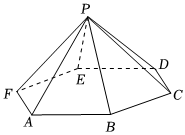21．如图，在正六棱锥P-ABCDEF中，球O是其内切球，
AB
=
2
，
PC
=
13
，点M是底面ABCDEF内一动点（含边界），且OM=OP．
（1）求正六棱锥P-ABCDEF的体积；
（2）当点M在底面ABCDEF内运动时，求线段OM所形成的曲面与底面ABCDEF所围成的几何体的表面积．
组卷：72引用：3难度：0.5
解析
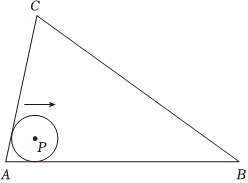22．已知△ABC的内角A，B，C所对边分别为a,b,c.若△ABC内部有一个圆心为P，半径为
3
米的圆，它沿着△ABC的边内侧滚动一周，且始终保持与三角形的至少一条边相切．
（1）若△ABC为边长是16米的等边三角形，求圆心P经过的路程；
（2）若用28米的材料刚好围成这个三角形，请你设计一种△ABC的围成方案，使得圆心P经过的路程最大并求出该最大值（若a,b,c为正数，则
a
+
b
+
c
≥
3
3
abc
，当且仅当a=b=c时取等号）．
组卷：33引用：1难度：0.5
解析