2023-2024学年四川省南充市仪陇中学高二（上）月考数学试卷（10月份）

一、单选题（每小题5分，共40分）

• 1．若z=（1-i）（2+i），则z的虚部为（　　）

  A．i

  B．-1

  C．1

  D．3
  组卷：23引用：3难度：0.8

  解析

• 2．下列给出的图形中，绕给出的轴旋转一周，能形成圆台的是（　　）

  A．

  B．

  C．

  D．
  组卷：139引用：6难度：0.8

  解析

• 3．已知角α终边上有一点

  P

  （

  3

  2

  ，

  1

  2

  ）

  ，则α为（　　）

  A．第一象限角

  B．第二象限角

  C．第三象限角

  D．第四象限角
  组卷：123引用：2难度：0.9

  解析

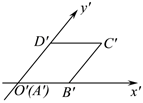• 4．一个水平放置的平面四边形ABCD采用斜二测画法得到的直观图是菱形A'B'C'D'，如图所示，则平面四边形ABCD的形状为（　　）

  A．正方形

  B．长方形

  C．菱形

  D．梯形
  组卷：148引用：4难度：0.7

  解析

• 5．已知a＞0，b＞0，且

  1

  a

  +

  2

  b

  =

  1

  ，则a+2b的最小值为（　　）

  A． 5 + 2 2

  B． 8 2

  C．5

  D．9
  组卷：123引用：4难度：0.5

  解析

• 6．已知正方体ABCD-A₁B₁C₁D₁的棱长为1，则点B到平面AB₁C的距离是（　　）

  A． 3 3

  B． 2 3 3

  C． 2

  D． 3
  组卷：20引用：3难度：0.7

  解析

• 7．计算

  y

  =

  sinx

  ,

  y

  =

  cosx

  ,

  y

  =

  e

  x

  ，

  y

  =

  lnx

  ,

  y

  =

  x

  等函数值时，计算器使用的是数值计算法，其中一种方法是用容易计算的多项式近似地表示这些函数，通过计算该多项式的值求出原函数近似值，如

  sinx

  =

  x

  -

  x

  3

  3

  !

  +

  x

  5

  5

  !

  -

  x

  7

  7

  !

  +

  ⋯

  ，

  cosx

  =

  1

  -

  x

  2

  2

  !

  +

  x

  4

  4

  !

  -

  x

  6

  6

  !

  +

  ⋯

  ，其中n!=n×⋯×3×2×1．英国数学家泰勒（B．Taylor,1685-1731）发现了这些公式，从中可以看出，右边的项用得越多，计算得出sinx和cosx的值也就越精确．运用上述思想，可得到

  sin

  （

  3

  π

  2

  -

  1

  ）

  的近似值为（　　）

  A．-0.50

  B．-0.52

  C．-0.54

  D．-0.56
  组卷：139引用：4难度：0.7

  解析

四、解答题（第17题10分，其余各题每题12分，共70分）

• 21．在四棱锥P-ABCD中，平面PAD⊥平面ABCD，底面ABCD为梯形，AB∥CD，AB⊥AD，且AB=1，PA=AD=DC=2，PD=2

  2

  ．
  （Ⅰ）求证：AB⊥PD；
  （Ⅱ）求二面角P-BC-D的余弦值．
  组卷：422引用：2难度：0.6

  解析

• 22．已知

  f

  （

  x

  ）

  =

  e

  x

  +

  1

  e

  x

  ，

  g

  （

  x

  ）

  =

  ln

  [

  （

  3

  -

  a

  ）

  e

  x

  +

  1

  ]

  -

  ln

  3

  a

  -

  2

  x

  ．
  （1）求函数f（x）在[0，+∞）的最小值．
  （2）对于任意x₁、x₂∈[0，+∞），都有g（x₁）≤f（x₂）-2成立，求a的取值范围．
  组卷：49引用：3难度：0.5

  解析