当前位置：试卷中心 > 试卷详情

2022-2023学年广东省佛山市南海外国语学校九年级（上）第三次月考数学试卷

发布：2024/8/19 14:0:1

一、选择题（共10小题，每小题3分，共30分）

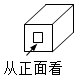1．如图，是一根空心方管，则它的左视图为（　　）
A． B． C． D．
组卷：98引用：5难度：0.8
解析
2．若关于x的一元二次方程x²-x+m=0的一个根是2，则m的值是（　　）
A．-1 B．-2 C．-3 D．2
组卷：461引用：14难度：0.6
解析
3．
3
tan
60
°
的值等于（　　）
A．1 B．
3
2
C．3 D．
3
组卷：617引用：5难度：0.7
解析
4．如图：AB∥CD∥EF，AD：DF=3：1，BE=12，那么CE的长为（　　）
A．3 B．4 C．5 D．6
组卷：3871引用：26难度：0.7
解析
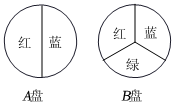5．用如图所示的A、B两个转盘进行“配紫色”游戏（红色和蓝色在一起配成紫色），A转盘是二等分，B转盘是三等分，分别转动两个转盘各一次（指针指向分界线则重新转动转盘），则配成紫色的概率为（　　）
A．
1
6
B．
1
4
C．
1
3
D．
1
2
组卷：374引用：9难度：0.6
解析
6．已知点A（-1，y₁）、B（-3，y₂）、C（
1
2
，y₃）在反比例函数y=-
6
x
的图象上，则y₁、y₂、y₃的大小关系正确的是（　　）
A．y₁＞y₂＞y₃ B．y₂＞y₁＞y₃ C．y₂＞y₃＞y₁ D．y₃＞y₁＞y₂
组卷：1430引用：8难度：0.6
解析
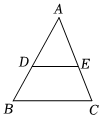7．如图，在△ABC中，D、E两点分别在AB、AC边上，DE∥BC，若AD：DB=3：2，则S_△ADE：S_△ABC为（　　）
A．3：5 B．9：4 C．9：25 D．3：2
组卷：113引用：3难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共8小题，16、17、18题每题8分，19、20、21题每题9分、22、23题每题12分，共75分）

22．小蒙在学习正方形时进行以下研究：

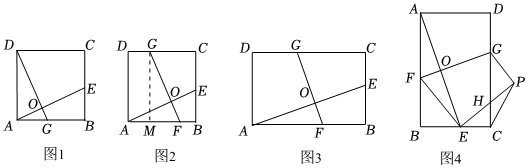
（1）如图（1），在正方形ABCD中，点E，Q分别在边BC，AB上，DQ⊥AE于点O，发现了AE=DQ，小蒙思考若点G，F，E分别在正方形ABCD的CD，AB，BC上，保持GF⊥AE，如图（2）所示，结论AE=GF还成立吗？请说明理由；（提示：过点G作GM⊥AB可构造△GMF≌△ABE）
（2）类比探究：如图（3），在矩形ABCD中，
BC
AB
=
k
（k为常数），点G，F，E分别在边CD，AB，BC上，GF⊥AE于点O，试探究GF与AE之间的数量关系，并说明理由；
（3）拓展应用：如图（4），将矩形ABCD沿GF折叠，使点A落在BC边上的点E处，得到四边形FEPG，EP交CD于点H，连接AE交GF于点O．若
sin
∠
BFE
=
4
5
，
AB
=
4
3
BC
，
FG
=
2
5
，则AB的长为
；点P到BC的距离为
．
组卷：96引用：2难度：0.5
解析
23．在平面直角坐标系中，点D是反比例函数y=
k
x
（k＞0）的一点，点D的纵坐标为6．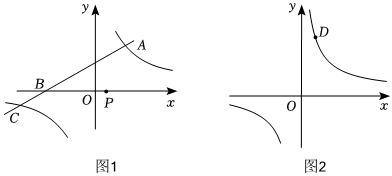

（1）当一次函数y=ax+3（a＞0）的图象与x轴交于点B（-6，0），与反比例函数y=
k
x
（k＞0）的图象交于A，C两点，点P（1，0）是x轴上一定点，已知点A的纵坐标为4．求一次函数和反比例函数的解析式；
（2）在（1）的条件下，在线段AB上找点Q使得△PAQ的面积为7时，求点Q的坐标；
（3）如图2，在第一象限内，在反比例函数上是否存在不同于点D的一点F，满足∠ODF=90°，且
tan
∠
DOF
=
1
4
，若存在求出点D的坐标．若不存在，请说明理由．
组卷：76引用：2难度：0.3
解析