小蒙在学习正方形时进行以下研究：
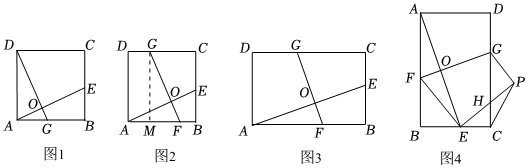
（1）如图（1），在正方形ABCD中，点E，Q分别在边BC，AB上，DQ⊥AE于点O，发现了AE=DQ，小蒙思考若点G，F，E分别在正方形ABCD的CD，AB，BC上，保持GF⊥AE，如图（2）所示，结论AE=GF还成立吗？请说明理由；（提示：过点G作GM⊥AB可构造△GMF≌△ABE）
（2）类比探究：如图（3），在矩形ABCD中，BCAB=k（k为常数），点G，F，E分别在边CD，AB，BC上，GF⊥AE于点O，试探究GF与AE之间的数量关系，并说明理由；
（3）拓展应用：如图（4），将矩形ABCD沿GF折叠，使点A落在BC边上的点E处，得到四边形FEPG，EP交CD于点H，连接AE交GF于点O．若sin∠BFE=45，AB=43BC，FG=25，则AB的长为 163163；点P到BC的距离为 165165．
BC
AB
=
k
sin
∠
BFE
=
4
5
AB
=
4
3
BC
FG
=
2
5
16
3
16
3
16
5
16
5
【考点】相似形综合题．
【答案】；
16
3
16
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/19 14:0:1组卷：106引用：2难度：0.5
相似题
-
1．数学课上，王老师出示问题：如图1，将边长为5的正方形纸片ABCD折叠，使顶点A落在边CD上的点P处（点P与C、D不重合），折痕为EF，折叠后AB边落在PQ的位置，PQ与BC交于点G．
（1）观察操作结果，在图1中找到一个与△DEP相似的三角形，并证明你的结论；
（2）当点P在边CD的什么位置时，△DEP与△CPG面积的比是9：25？请写出求解过程；
（3）将正方形换成正三角形，如图2，将边长为5的正三角形纸片ABC折叠，使顶点A落在边BC上的点P处（点P与B、C不重合），折痕为EF，当点P在边BC的什么位置时，△BEP与△CPF面积的比是9：25？请写出求解过程．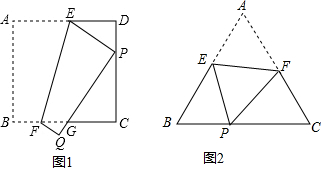
发布：2025/6/15 22:0:1组卷：1072引用：9难度：0.2 -
2．在矩形ABCD中，AD=3，CD=4，点E在边CD上，且DE=1．
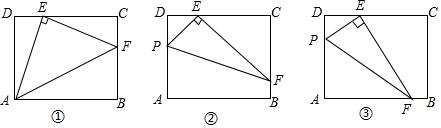
感知：如图①，连接AE，过点E作EF⊥AE，交BC于点F，连接AF，易证：△ADE≌△ECF（不需要证明）；
探究：如图②，点P在矩形ABCD的边AD上（点P不与点A、D重合），连接PE，过点E作EF⊥PE，交BC于点F，连接PF．求证：△PDE∽△ECF；
应用：如图③，若EF交AB边于点F，其他条件不变，且△PEF的面积是3，则AP的长为．发布：2025/6/16 19:30:1组卷：681引用：3难度：0.1 -
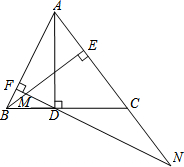3．如图，AD、BE是△ABC的两条高，过点D作DF⊥AB，垂足为F，FD交BE于M，FD、AC的延长线交于点N．
（1）求证：△BFM∽△NFA；
（2）试探究线段FM、DF、FN之间的数量关系，并证明你的结论；
（3）若AC=BC，DN=12，ME：EN=1：2，求线段AC的长．发布：2025/6/16 11:30:2组卷：851引用：7难度：0.3
