2023-2024学年四川省成都七中高二(上)段考数学试卷(10月份)
发布:2024/9/22 15:0:8
一、单选题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1.已知点
,点A(0,3),则直线AB的倾斜角为( )B(-1,23)组卷:30引用:7难度:0.9 -
2.已知直线a,b的方向向量分别为
,a=(1,0,-1),且直线a,b均平行于平面α,平面α的单位法向量为( )b=(1,-1,0)组卷:51引用:4难度:0.7 -
3.有2人从一座6层大楼的底层进入电梯,假设每个人自第二层开始在每一层离开电梯是等可能的,则该2人在不同层离开电梯的概率是( )
组卷:89引用:5难度:0.7 -
 4.如图,在斜棱柱ABCD-A1B1C1D1中,AC与BD的交点为点M,,AB=a,AD=b,则AA1=c=( )MC1组卷:1440引用:24难度:0.8
4.如图,在斜棱柱ABCD-A1B1C1D1中,AC与BD的交点为点M,,AB=a,AD=b,则AA1=c=( )MC1组卷:1440引用:24难度:0.8 -
5.某校高一年级15个班参加合唱比赛,得分从小到大排序依次为:85,85,86,87,88,89,90,91,91,91,92,93,94,96,98,则这组数据的80%分位数是( )
组卷:140引用:3难度:0.8 -
6.四名同学各掷骰子5次,分别记录每次骰子出现的点数,根据四名同学的统计结果、可以判断出一定没有出现点数6的是( )
组卷:250引用:9难度:0.7 -
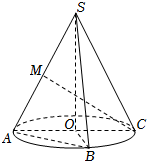 7.如图,某圆锥SO的轴截面SAC,其中SA=AO,点B是底面圆周上的一点,且cos∠BOC=5,点M是线段SA的中点,则异面直线SB与CM所成角的余弦值是( )23组卷:122引用:5难度:0.6
7.如图,某圆锥SO的轴截面SAC,其中SA=AO,点B是底面圆周上的一点,且cos∠BOC=5,点M是线段SA的中点,则异面直线SB与CM所成角的余弦值是( )23组卷:122引用:5难度:0.6
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
-
 21.在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥AB,侧面PAB⊥底面ABCD,PA=PB=AD=BC=2,且E,F分别为PC,CD的中点.12
21.在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥AB,侧面PAB⊥底面ABCD,PA=PB=AD=BC=2,且E,F分别为PC,CD的中点.12
(1)证明:DE∥平面PAB;
(2)若直线PF与平面PAB所成的角为60°,求平面PAB与平面PCD所成锐二面角的余弦值.组卷:288引用:26难度:0.6 -
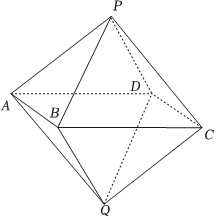 22.如图,在八面体PABCDQ中,四边形ABCD是边长为2的正方形,平面PAD∥平面QBC,二面角P-AB-C与二面角Q-CD-A的大小都是30°,,PD⊥AB.AP=CQ=3
22.如图,在八面体PABCDQ中,四边形ABCD是边长为2的正方形,平面PAD∥平面QBC,二面角P-AB-C与二面角Q-CD-A的大小都是30°,,PD⊥AB.AP=CQ=3
(1)证明:平面PCD∥平面QAB;
(2)设G为△QBC的重心,是否在棱PA上存在点S,使得SG与平面ABCD所成角的正弦值为,若存在,求S到平面ABCD的距离,若不存在,说明理由.3020组卷:144引用:6难度:0.5


