2022-2023学年山东省临沂市沂水县八年级（下）期末数学试卷
发布：2024/6/29 8:0:10
一、选择题。（本大题共12小题，每小题3分，共36分）在每小题所给出的四个选项中，只有一项是符合题目要求的。）
-
1．如果
是最简二次根式，则x的值可能是（ ）x-5组卷：41引用：3难度：0.7 -
2．祖冲之是中国数学史上伟大的数学家，他把圆周率精确到小数点后7位，这是祖冲之最重要的数学贡献．数学活动课上，同学们对圆周率的小数点后100位数字进行了统计：
那么，圆周率的小数点后100位数字的众数为（ ）数字 0 1 2 3 4 5 6 7 8 9 频数 8 8 12 11 10 8 9 8 12 14 组卷：80引用：4难度：0.8 -
3．把
根号外的因式移进根号内，结果等于（ ）-2212组卷：77引用：2难度：0.7 -
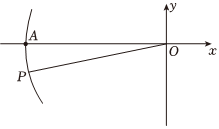4．如图，以点O为圆心，以OP的长为半径画弧，交x轴的负半轴于点A．若点A的坐标为，P点的纵坐标为-1，则P点的横坐标为（ ）（52，0）
组卷：44引用：1难度：0.5 -
5．骆驼被称为“沙漠之舟”，它的体温随时间的变化而发生较大的变化，如图所示，下列说法错误的是（ ）
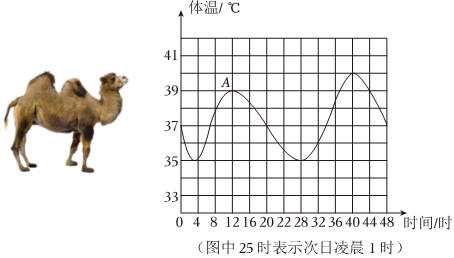组卷：120引用：2难度：0.7 -
6．育新中学八年级六班有53人．一次月考后，数学老师对数学成绩进行了统计．由于有三人因事没有参加本次月考，因此计算其他50人的平均分为90分，方差s2=40．后来三进行了补考，数学成绩分别为88分，90分，92分．加入这三人的成绩后，下列说法正确的是（ ）
组卷：19引用：2难度：0.7 -
7．下列关于一次函数y=-2x+2的说法中，错误的是（ ）
组卷：76引用：2难度：0.5
三、解答题。（本大题共7小题，共72分）
-
22．刻漏是人类最早制造的不完全依赖天象、相对独立运行的计时仪器．刻漏以水等液体（也有少数例外，如水银或沙等）为工作物质，根据流水的量与流逝时间的对应关系，通过漏壶中的水量变化来度量时间的．我国使用刻漏的时间非常早，最早可追溯到中国历史上第一个王朝一夏朝（大约公元前2070年），约在汉武帝时期发明了浮箭漏．如图所示为单级浮箭漏示意图．某兴趣小组仿制了一套浮箭漏，并从函数角度进行了如下实验探究：
【实验观察】实验小组通过观察，每1小时记录一次箭尺读数，得到如表：
【探索发现】（1）在所给的平面直角坐标系中，描出以供水时间x为横坐标，箭尺读数y为纵坐标的各点．供水时间x（小时） 0 1 2 3 4 箭尺读数y（厘米）6 6 12 18 24 30
（2）观察上述各点的分布规律，判断它们是否在同一条直线上，如果在同一条直线上，求出这条直线所对应的函数表达式，如果不在同一条直线上，说明理由；
【结论应用】应用上述发现的规律估算：
（3）供水时间达到10小时时，箭尺的读数为多少厘米？
（4）如果本次实验记录的开始时间是上午7：30，那当箭尺读数为96厘米时是几点钟？（箭尺最大读数为100厘米）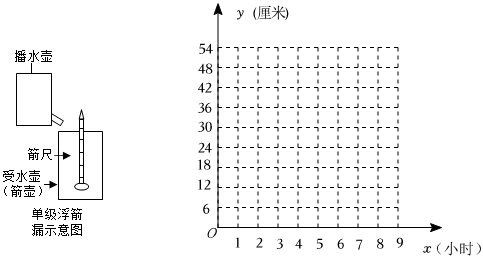
组卷：343引用：4难度：0.6 -
23．综合与实践
问题：给你两个大小不等的正方形，你能通过切割把他们拼接成一个大正方形吗？
下面是某研究小组的研究过程：
（1）首先研究两个一样大小的正方形
把两个边长相等的正方形ABCD和EFGH，按图1所示的方式摆放，沿虚线BD、EG剪开后，可按图1所示的移动方式拼接成四边形形BNED，则四边形形BNED是正方形，请说明理由；
（2）研究大小不等的两个正方形
把边长不等的两个正方形ABCD和EFGH，按图2所示的方式摆放，连接DE，过点D作DM⊥DE，交AB于点M，过点M作 MN⊥DM，过点E作EN⊥DE，MN与EN相交于点N．
①证明四边形MNED是正方形；
②在图2中，将正方形ABCD和正方形EFGH沿虚线剪开后，能够拼接为正方形MNED，请简略说明你的拼接方法．（类比图1，用数字表示对应的图形）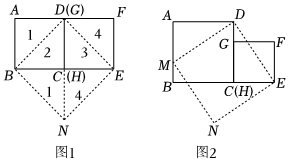
组卷：63引用：1难度：0.4
