2022-2023学年黑龙江省鹤岗一中高二（上）期末数学试卷

一、单选题（本题共8小题，每小题5分，共40分）

• 1．抛物线y=4x²的焦点坐标是（　　）

  A．（0，1）

  B．（1，0）

  C． （ 0 ， 1 16 ）

  D． （ 1 16 ， 0 ）
  组卷：585引用：169难度：0.9

  解析

• 2．设双曲线

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的一个焦点到一条渐近线的距离等于

  3

  2

  c,则该双曲线的渐近线方程为（　　）

  A． 3 y±x=0

  B．y±2x=0

  C．x±2y=0

  D．y± 3 x=0
  组卷：34引用：2难度：0.7

  解析

• 3．2022年8月某市组织应急处置山火救援行动，现从组织好的5支志愿团队中任选1支救援物资接收点服务，另外4支志愿团队分配给“传送物资、砍隔离带、收捡垃圾”三个不同项目，每支志愿团队只能分配到1个项目，且每个项目至少分配1个志愿团队，则不同的分配方案种数为（　　）

  A．36

  B．81

  C．120

  D．180
  组卷：142引用：3难度：0.7

  解析

• 4．近年来，淮南市全力推进全国文明城市创建工作，构建良好的宜居环境，城市公园越来越多，某周末，甲、乙两位市民准备从龙湖公园、八公山森林公园、上密森林公园、山南中央公园4个景点中随机选择其中一个景点游玩，记事件M：甲和乙至少一人选择八公山森林公园，事件N：甲和乙选择的景点不同，则P（N|M）=（　　）

  A． 7 16

  B． 7 8

  C． 3 7

  D． 6 7
  组卷：307引用：2难度：0.7

  解析

• 5．下列说法不正确的是（　　）

  A．在回归直线方程 ̂ y = - 0 . 85 x + 2 . 3 中，y与x具有负线性相关关系

  B．两个随机变量的线性相关性越强，则相关系数的绝对值就越大

  C．随机变量X服从正态分布N（4，1），若P（X≥5）=0.2，则P（3＜X＜5）=0.6

  D．已知随机变量X服从二项分布B（n,p），若E（X）=30，D（X）=20，则 p = 2 3
  组卷：139引用：2难度：0.6

  解析

• 6．点M为抛物线y²=8x上任意一点，点N为圆x²+y²-4x+3=0上任意一点，P为直线ax-y-a-1=0的定点，则|MP|+|MN|的最小值为（　　）

  A．2

  B． 2

  C．3

  D． 2 + 2
  组卷：45引用：2难度：0.6

  解析

• 7．设椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左、右焦点分别为F₁、F₂，其焦距为2c,点Q（c,

  a

  2

  ）在椭圆的外部，点P是椭圆C上的动点，且

  |

  P

  F

  1

  |

  +

  |

  PQ

  |

  ＜

  3

  2

  |

  F

  1

  F

  2

  |

  恒成立，则椭圆离心率的取值范围是（　　）

  A． （ 2 2 ， 5 6 ）

  B． （ 2 2 ， 3 4 ）

  C． （ 5 6 ， 1 ）

  D． （ 3 4 ， 1 ）
  组卷：280引用：3难度：0.7

  解析

四、解答题（本题共6道小题，共计70分.解答应写出文字说明，证明过程或演算步骤）

• 21．4月23日是联合国教科文组织确定的“世界读书日”．为了解某地区高一学生阅读时间的分配情况，从该地区随机抽取了500名高一学生进行在线调查，得到了这500名学生的日平均阅读时间（单位：小时），并将样本数据分成[0，2]，（2，4]，（4，6]，（6，8]，（8，10]，（10，12]，（12，14]，（14，16]，（16，18]九组，绘制成如图所示的频率分布直方图．
  
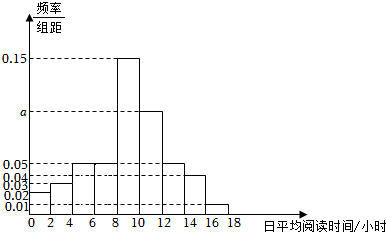
  （1）从这500名学生中随机抽取一人，日平均阅读时间在（10，12]内的概率；
  （2）为进一步了解这500名学生数字媒体阅读时间和纸质图书阅读时间的分配情况，从日平均阅读时间在（12，14]，（14，16]，（16，18]三组内的学生中，采用分层抽样的方法抽取了10人，现从这10人中随机抽取3人，记日平均阅读时间在（14，16]内的学生人数为X，求X的分布列和数学期望；
  （3）以样本的频率估计概率，从该地区所有高一学生中随机抽取10名学生，用P（k）表示这10名学生中恰有k名学生日平均阅读时间在（8，12]内的概率，其中k=0，1，2，…，10．当P（k）最大时，写出k的值．（只需写出结论）
  组卷：216引用：2难度：0.6

  解析

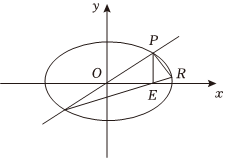• 22．在平面直角坐标系xOy中，过方程mx²+ny²=1（m,n∈R，m,n≠0）所确定的曲线C上点M（x₀，y₀）的直线与曲线C相切，则此切线的方程mx₀x+ny₀y=1．
  （1）若m=n=

  1

  4

  ，直线l过（

  3

  ，2）点被曲线C截得的弦长为2，求直线l的方程；
  （2）若m=l,n=-

  1

  3

  ，点A是曲线C上的任意一点，曲线过点A的切线交直线l₁：

  3

  x-y=0于M，交直线l₂：

  3

  x+y=0于N，证明：

  MA

  +

  NA

  =

  0

  ；
  （3）若m=

  1

  4

  ，n=

  1

  2

  ，过坐标原点斜率k＞0的直线l₃交C于P、Q两点，且点P位于第一象限，点P在x轴上的投影为E，延长QE交C于点R，求

  PQ

  •

  PR

  的值．
  组卷：43引用：2难度：0.5

  解析