2022-2023学年安徽省合肥市庐江县高一（下）期末数学试卷

一、选择题：（本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.）

• 1．为了扎实推进“五大行动”，学校为高一年级同学准备了形式多样的劳动课程．有种植白菜、种植番茄、果树整枝和害虫防治4种课程，小明要随机选报其中的2个，则该试验中样本点的个数为（　　）

  A．3

  B．5

  C．6

  D．9
  组卷：9引用：1难度：0.7

  解析

• 2．已知i为虚数单位，复数z满足|z+2i|=|z|，则z的虚部为（　　）

  A．-1

  B．-2

  C．1

  D．2
  组卷：40引用：1难度：0.8

  解析

• 3．不同的直线m和n,不同的平面α，β，γ，下列条件中能推出α∥β的是（　　）

  A．α∩γ=n,β∩γ=m,n∥m	B．α⊥γ，β⊥γ
  C．n∥m,n⊥α，m⊥β	D．n∥α，m∥β，n∥m
  组卷：618引用：6难度：0.9

  解析

• 4．某企业为响应国家新旧动能转换的号召，积极调整企业拥有的5种系列产品的结构比例，并坚持自主创新提升产业技术水平，2021年年总收入是2020年的2倍，为了更好的总结5种系列产品的年收入变化情况，统计了这两年5种系列产品的年收入构成比例，得到如图饼图：
  
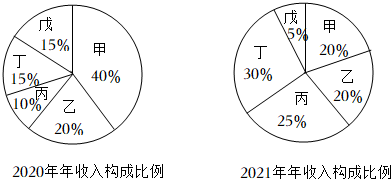
  则下列结论错误的是（　　）

  A．2021年的甲系列产品收入和2020年保持不变

  B．2021年的丁系列产品收入是2020年丁系列产品收入的4倍

  C．2021年的丙和丁系列产品的收入之和比2020年的企业年总收入还多

  D．2021年的乙和丙系列产品的收入之和比2020年的乙和丙系列产品收入之和的2倍还少
  组卷：151引用：3难度：0.8

  解析

• 5．已知两座灯塔A和B与海洋观察站C的距离都等于20km,灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与灯塔B的距离为（　　）

  A．20km

  B． 20 2 km

  C． 20 3 km

  D． 15 5 km
  组卷：40引用：1难度：0.8

  解析

• 6．已知圆锥的顶点为S，底面圆心为O，以过SO的平面截该圆锥，所得截面为一个面积为4的等腰直角三角形，则该圆锥的侧面积为（　　）

  A． 4 2 π

  B． 8 2 π

  C．8π

  D．16π
  组卷：278引用：5难度：0.7

  解析

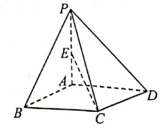• 7．在《九章算术》中，将底面为矩形且有一条侧棱与底面垂直的四棱锥称为“阳马”．如图，四棱锥P-ABCD为阳马，侧棱PA⊥底面ABCD，PA=AB=AD，E为棱PA的中点，则直线CE与平面PAD所成角的正弦值为（　　）

  A． 2 3

  B． 5 3

  C． 3 2

  D． 2 2
  组卷：1120引用：11难度：0.5

  解析

四、解答题（本大题共6小题，第17题10分，第18-22题每题12分，共70分，解答应写成文字说明、证明过程或演算步骤）

• 21．在△ABC中，角A，B，C所对的边长为a,b,c,b=a+1，c=a+2．
  （1）若2sinC=3sinA，求△ABC的面积；
  （2）是否存在正整数a,使得△ABC为钝角三角形？若存在，求出a的值；若不存在，说明理由．
  组卷：9555引用：33难度：0.5

  解析

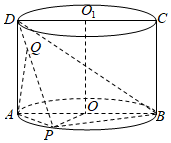• 22．如图，四边形ABCD是圆柱OO₁的轴截面，点P为底面圆周上异于A，B的点．
  （1）求证：PB⊥平面PAD；
  （2）若圆柱的侧面积为2π，体积为π，点Q为线段DP上靠近点D的三等分点，是否存在一点P使得直线AQ与平面BDP所成角的正弦值最大？若存在，求出相应的正弦值，并指出点P的位置；若不存在，说明理由．
  组卷：209引用：4难度：0.4

  解析