2022-2023学年四川省绵阳市涪城区跃进北路学校九年级（上）第一次月考数学试卷

一、选择题：共36分.

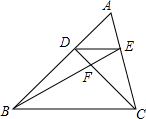• 1．如图，在△ABC中，D、E分别是AB、AC上的点，DE∥BC，BE与CD相交于F，则下列结论一定正确的是（　　）

  A． AD BD = DE BC

  B． AD AB = AE AC

  C． DF FC = AE EC

  D． DF BF = EF FC
  组卷：1193引用：14难度：0.7

  解析

• 2．已知：在Rt△ABC中，∠C=90°，sinA=

  3

  4

  ，则cosB的值为（　　）

  A． 7 4

  B． 3 4

  C． 3 5

  D． 4 5
  组卷：1180引用：8难度：0.7

  解析

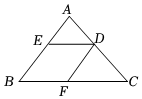• 3．如图，四边形BEDF是菱形，延长BE至点A，延长BF至点C，使得AC经过点D，若AE=3，BE=4，则FC的长为（　　）

  A． 4 3

  B． 8 3

  C． 16 3

  D． 28 3
  组卷：20引用：3难度：0.5

  解析

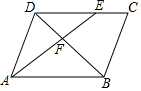• 4．如图，在平行四边形ABCD中，E是DC上的点，DE：EC=3：2，连接AE交BD于点F，则△DEF与△BAF的面积之比为（　　）

  A．2：5

  B．3：5

  C．9：25

  D．4：25
  组卷：2926引用：28难度：0.8

  解析

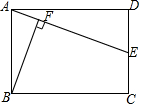• 5．如图，在矩形ABCD中，AB=2，BC=3．若点E是边CD的中点，连接AE，过点B作BF⊥AE交AE于点F，则BF的长为（　　）

  A． 3 10 2

  B． 3 10 5

  C． 10 5

  D． 3 5 5
  组卷：9362引用：36难度：0.7

  解析

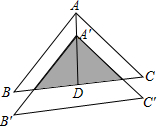• 6．如图，将△ABC沿BC边上的中线AD平移到△A'B'C'的位置，已知△ABC的面积为9，阴影部分三角形的面积为4．若AA'=1，则A'D等于（　　）

  A．2

  B．3

  C． 2 3

  D． 3 2
  组卷：3143引用：20难度：0.7

  解析

• 7．点M（tan60°，-cos60°）关于y轴的对称点是（　　）

  A．（- 3 ， 1 2 ）

  B．（ 3 ， 1 2 ）

  C．（ 3 ，- 1 2 ）

  D．（- 3 ，- 1 2 ）
  组卷：118引用：3难度：0.9

  解析

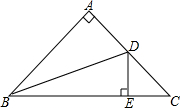• 8．如图，在△ABC中，∠BAC=90°，AB=AC，点D为边AC的中点，DE⊥BC于点E，连接BD，则tan∠DBC的值为（　　）

  A． 1 3

  B． 2 -1

  C．2- 3

  D． 1 4
  组卷：7979引用：79难度：0.9

  解析

三、解答题：共66分

• 25．综合与实践
  综合与实践课上，老师让同学们以“图形的变换”为主题开展数学活动．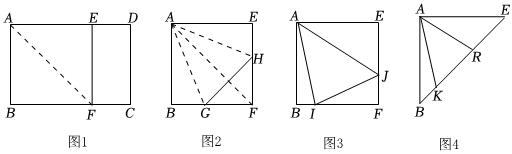
  （1）操作判断如图1，将矩形纸片ABCD折叠，使AB落在边AD上，点B与点E重合，折痕为AF，即可得到正方形AEFB，沿EF剪开，将正方形AEFB折叠使边AB，AE都落在正方形的对角线AF上，折痕为AG，AH，连接GH，如图2．根据以上操作，则∠GAH=

  °．
  （2）迁移探究
  将图2中的∠GAH绕点A按顺时针旋转，使它的两边分别交边BF，FE于点I，J，连接IJ，
  如图3．探究线段BI，IJ，EJ之间的数量关系，并说明理由．
  （3）拓展应用
  连接正方形对角线BE，若图3中的∠IAJ的边AI，AJ分别交对角线BE于点K，R，将正方形纸片沿对角线BE剪开，如图4，若BK=2，ER=4，请直接写出KR的长．
  组卷：233引用：10难度：0.4

  解析

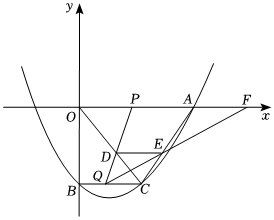• 26．如图，在平面直角坐标系xOy中，抛物线y=

  1

  18

  x²-

  4

  9

  x-10与y轴的交点为点B，过点B作x轴的平行线BC，交抛物线于点C，连接AC．现有两动点P，Q分别从O，C两点同时出发，点P以每秒4个单位的速度沿OA向终点A移动，点Q以每秒1个单位的速度沿CB向点B移动，点P停止运动时，点Q也同时停止运动，线段OC，PQ相交于点D，过点D作DE∥OA，交CA于点E，射线QE交x轴于点F．设动点P，Q移动的时间为t（单位：秒）．
  （1）求A，B，C三点的坐标和抛物线的顶点坐标；
  （2）当0＜t＜

  9

  2

  时，△PQF的面积是否总为定值？若是，求出此定值，若不是，请说明理由；
  （4）当t为何值时，△PQF为等腰三角形？请写出解答过程．
  组卷：54引用：2难度：0.3

  解析