综合与实践
综合与实践课上，老师让同学们以“图形的变换”为主题开展数学活动．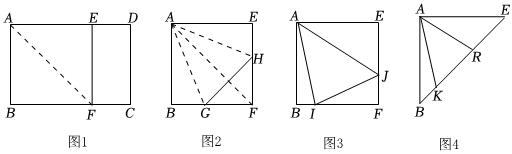
（1）操作判断如图1，将矩形纸片ABCD折叠，使AB落在边AD上，点B与点E重合，折痕为AF，即可得到正方形AEFB，沿EF剪开，将正方形AEFB折叠使边AB，AE都落在正方形的对角线AF上，折痕为AG，AH，连接GH，如图2．根据以上操作，则∠GAH=4545°．
（2）迁移探究
将图2中的∠GAH绕点A按顺时针旋转，使它的两边分别交边BF，FE于点I，J，连接IJ，
如图3．探究线段BI，IJ，EJ之间的数量关系，并说明理由．
（3）拓展应用
连接正方形对角线BE，若图3中的∠IAJ的边AI，AJ分别交对角线BE于点K，R，将正方形纸片沿对角线BE剪开，如图4，若BK=2，ER=4，请直接写出KR的长．
【考点】几何变换综合题．
【答案】45
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/15 12:0:2组卷：233引用：10难度：0.4
相似题
-
1．【发现奥秘】
（1）如图1，在等边三角形ABC中，AB=2，点E是△ABC内一点，连接AE，EC，BE，分别将AC，EC绕点C顺时针旋转60°得到DC，FC，连接AD，DF，EF．当B，E，F，D四个点满足 时，BE+AE+CE的值最小，最小值为 ．
【解法探索】
（2）如图2，在△ABC中，∠ACB=90°，AC=BC，点P是△ABC内一点，连接PA，PB，PC，请求出当PA+PB+PC的值最小时∠BCP的度数，并直接写出此时PA：PB：PC的值．（提示：分别将PC，AC绕点C顺时针旋转60°得到DC，EC，连接PD，DE，AE）
【拓展应用】
（3）在△ABC中，∠ACB=90°，∠BAC=30°，BC=2，点P是△ABC内一点，连接PA，PB，PC，直接写出当PA+PB+PC的值最小时，PA：PB：PC的值．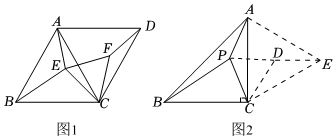
发布：2025/5/26 0:30:1组卷：232引用：1难度：0.4 -
2．下面是某数学兴趣小组对一个数学问题作的探究活动：
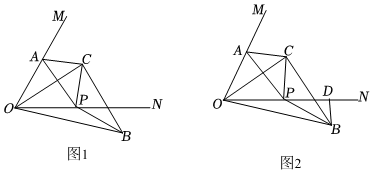
（1）如图1，小明同学得出△OAC≌△BPC，他的判断理由是 ．问题：
如图1，已知，∠MON=60°，点A在边OM上，点P是边ON上一动点，以线段AP为斜边作Rt△ACP，AC=PC，∠ACP=90°（C和O在AP的两侧），连接OC，将线段OC绕C逆时针旋转90°至BC，连接OB．
A．SSS
B．SAS
C．AAS
D．ASA
（2）如图2，小颖同学作BD⊥ON于D，她认为OA与BD存在某种数量关系，那么OA与BD是否有数量关系？如果有数量关系，请你写出OA与BD的数量关系并说明理由；
（3）如图1，小华说，当OA=2，当△AOP是直角三角形时，可求出OB2的值，请你直接写出OB2的值．发布：2025/5/25 22:30:2组卷：142引用：2难度：0.1 -
3．如图1，在等腰直角三角形ABC中，∠BAC=90°，点E，F分别为AB，AC的中点，H为线段EF上一动点（不与点E，F重合），将线段AH绕点A逆时针方向旋转90°得到AG，连接GC，HB．
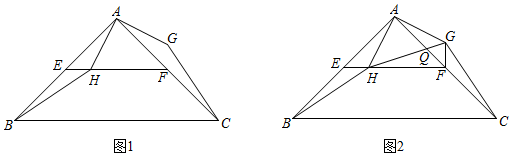
（1）证明：△AHB≌△AGC；
（2）如图2，连接GF，HG，HG交AF于点Q．①证明：在点H的运动过程中，总有∠HFG=90°；②若AG=QG，AB=AC=4，求EH的长度．发布：2025/5/26 1:0:1组卷：181引用：1难度：0.3
