2022-2023学年广东省惠州市惠阳区竹贤学校八年级（上）月考数学试卷（10月份）
发布：2024/8/20 20:0:1
一、选择题（共10题，共30分）
-
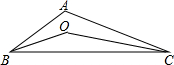1．如图，△ABC的角平分线BO、CO相交于点O，∠A=120°，则∠BOC=（ ）组卷：374引用：10难度：0.9 -
2．下列航空公司的标志中，是轴对称图形的是（ ）
组卷：2930引用：20难度：0.9 -
3．下列图形中，是轴对称图形的为（ ）
组卷：292引用：22难度：0.9 -
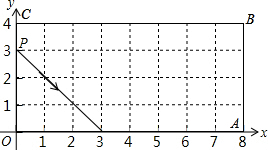4．如图，在4×8的长方形网格OABC中，动点P从（0，3）出发，沿箭头所示方向运动，每当碰到长方形的边时反弹，反弹时反射角等于入射角，当点P第2020次碰到矩形的边时，点P的坐标为（ ）组卷：611引用：3难度：0.4 -
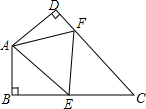5．如图，四边形ABCD中，∠C=50°，∠B=∠D=90°，E、F分别是BC、DC上的点，当△AEF的周长最小时，∠EAF的度数为（ ）组卷：10754引用：73难度：0.9 -
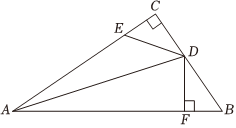6．如图，在Rt△ABC中．∠C=90°，D是BC上一点．E是AC上一点．DF⊥AB，若DB=ED，EC=FB，则下列结论：①DC=DF；②AD平分∠CAB；③AC=AD；④AE+AB=2AC中．正确的结论有（ ）组卷：23引用：2难度：0.5 -
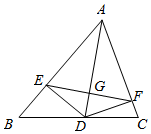7．如图，AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，连接EF交AD于点G，则下列结论：①DF+AE＞AD；②DE=DF；③AD⊥EF；④S△ABD：S△ACD=AB：AC，其中正确结论的个数是（ ）组卷：2287引用：9难度：0.4 -
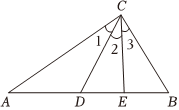8．如图△ABC中，∠A：∠B：∠ACB=1：2：3，∠1=∠2=∠3，则AD：DE：EB为（ ）组卷：65引用：2难度：0.7
三、解答题（共8题，共62分）
-
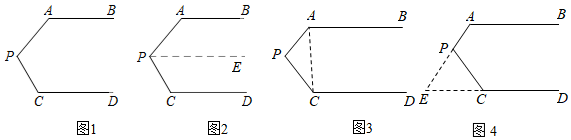
24．问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC度数．
思路点拨：
小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可分别求出∠APE、∠CPE的度数，从而可求出∠APC的度数；
小丽的思路是：如图3，连接AC，通过平行线性质以及三角形内角和的知识可求出∠APC的度数；
小芳的思路是：如图4，延长AP交DC的延长线于E，通过平行线性质以及三角形外角的相关知识可求出∠APC的度数．
问题解决：请从小明、小丽、小芳的思路中任选一种思路进行推理计算，你求得的∠APC的度数为°；
问题迁移：（1）如图5，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP=∠α，∠BCP=∠β．∠CPD、∠α、∠β之间有何数量关系？请说明理由；
（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．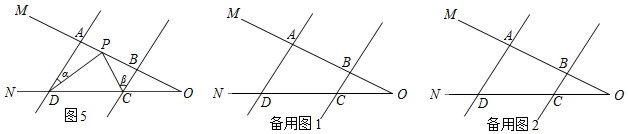
组卷：575引用：5难度：0.5 -
25．（1）尺规作图：如图a,已知∠MON，作∠MON的平分线OP，并在OP上任取一点Q，分别在OM、ON上各取一点S、T，作△OSQ和△OTQ，使得△OSQ≌△OTQ．（不写作法，保留作图痕迹）
（2）请你参考这个作全等三角形的方法，解答下列问题：
①如图b,在△ABC中，∠ACB是直角，∠B=60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F．请你判断并写出FE与FD之间的数量关系；
②如图c,在△ABC中，如果∠ACB不是直角，而①中的其它条件不变，请问，你在①中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由．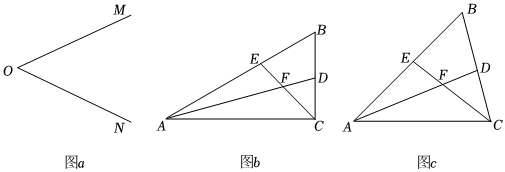
组卷：173引用：2难度：0.3
