2022-2023学年浙江省宁波市高二（下）期末数学试卷

一、单项选择题（本大题共12小题，每小题3分，共36分.每小题列出的四个备选项中只有一个是符合题目要求的，不选、多选、错选均不得分.

• 1．已知集合A={0，1，2}，B={-1，0}，则A∪B=（　　）

  A．{-1，1，2}

  B．{0，1，2}

  C．{-1，0}

  D．{-1，0，1，2}
  组卷：146引用：5难度：0.8

  解析

• 2．复数-1-2i（i为虚数单位）的虚部是（　　）

  A．-2

  B．-1

  C．1

  D．2
  组卷：29引用：3难度：0.8

  解析

• 3．函数

  f

  （

  x

  ）

  =

  （

  x

  -

  1

  2

  ）

  1

  2

  的定义域是（　　）

  A． （ - ∞ ， 1 2 ）

  B． [ 1 2 ， + ∞ ）

  C． { - ∞ ，- 1 2 }

  D． [ - 1 2 ， + ∞ ）
  组卷：374引用：7难度：0.7

  解析

• 4．已知tanα=-1，α∈（0，π]，那么α的值等于（　　）

  A． π 6

  B． π 4

  C． π 3

  D． 3 π 4
  组卷：51引用：3难度：0.9

  解析

• 5．某制药厂正在测试一种减肥药的疗效，有1000名志愿者服用此药，结果如表：
  

  体重变化	体重减轻	体重不变	体重增加
  人数	241	571	188

  如果另有一人服用此药，根据上表数据估计此人体重减轻的概率是（　　）

  A．0.57

  B．0.33

  C．0.24

  D．0.19
  组卷：37引用：2难度：0.8

  解析

• 6．已知向量

  a

  =（x,2），

  b

  =（3，6），

  a

  ⊥

  b

  ，则实数x的值为（　　）

  A．1

  B．-4

  C．4

  D．-1
  组卷：126引用：3难度：0.7

  解析

• 7．球的半径是R=3，则该球的体积是（　　）

  A．36π

  B．20π

  C．25π

  D．30π
  组卷：134引用：3难度：0.9

  解析

• 8．对数lga与lgb互为相反数，则有（　　）

  A．a+b=0

  B．a-b=0

  C．ab=1

  D． a b = 1
  组卷：1390引用：11难度：0.9

  解析

• 9．取一条长度为1的线段，将它三等分，去掉中间一段，留下剩下的两段；再将剩下的两段分别分割三等分，各去掉中间一段，留剩下的更短的四段；…；将这样的操作一直继续下去，直至无穷，由于在不断分割舍弃过程中，所形成的线段数目越来越多，长度越来越小，在极限的情况下，得到一个离散的点集，称为康托尔三分集．若在第n次操作中去掉的线段长度之和不小于

  1

  60

  ，则n的最大值为（　　）​（参考数据：1.5⁷≈17.1，1.5⁸≈25.6，1.5⁹≈38.4，1.5¹⁰≈57.7）

  A．7

  B．8

  C．9

  D．10
  组卷：65引用：3难度：0.5

  解析

六、解答题（本大题共2小题，共30分，解答应写出文字说明、证明过程或演算步骤，）

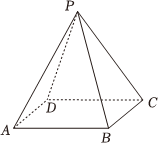• 28．如图，正四棱锥P-ABCD的高为

  2

  2

  ，体积为

  8

  2

  3

  ．
  （1）求正四棱锥P-ABCD的表面积；
  （2）若点E为线段PB的中点，求直线AE与平面ABCD所成角的正切值；
  （3）求二面角A-PB-C的余弦值．
  组卷：76引用：2难度：0.5

  解析

• 29．已知定义在R上的函数f（x）=-x²+x|x-a|，其中a为实数．
  （1）当a=3时，解不等式f（x）≥-2；
  （2）若函数f（x）在[-1，1]上有且仅有两个零点，求a的取值范围；
  （3）对于a∈[4，+∞），若存在实数x₁，x₂（x₁＜x₂），满足f（x₁）=f（x₂）=m,求

  x

  2

  1

  +

  m

  x

  2

  x

  1

  x

  2

  的取值范围．（结果用a表示）
  组卷：32引用：2难度：0.2

  解析