2022-2023学年浙江省绍兴市诸暨市八年级（下）期末数学试卷

一、选择题（共10小题，每题3分，共计30分）

• 1．下列x的取值中，可以使

  7

  -

  x

  有意义的是（　　）

  A．0

  B．16

  C．20

  D．2023
  组卷：47引用：1难度：0.8

  解析

• 2．下列四个图形中，既是中心对称图形，又是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：685引用：18难度：0.8

  解析

• 3．设方程x²-3x+c=0的两根分别是x₁，x₂，则x₁+x₂的值是（　　）

  A．-3

  B．3

  C．-6

  D．6
  组卷：195引用：1难度：0.6

  解析

• 4．若点A（a,b）在反比例函数y=

  2

  x

  的图象上，则代数式ab-5的值为（　　）

  A．-3

  B．0

  C．2

  D．-5
  组卷：622引用：4难度：0.8

  解析

• 5．在学校的体育训练中，李明投掷实心球的7次成绩如下表所示，则这7次成绩的中位数是（　　）
  

  次数	1	2	3	4	5	6	7
  成绩/米	9.7	9.6	9.8	10	9.8	9.9	10.1

  A．9.6米

  B．9.7米

  C．9.8米

  D．9.9米
  组卷：193引用：3难度：0.7

  解析

• 6．下列说法中正确的是（　　）

  A．有一个角是直角的四边形是矩形

  B．四边相等的四边形是矩形

  C．对角线互相垂直的平行四边形是矩形

  D．对角线相等的平行四边形是矩形
  组卷：1117引用：4难度：0.5

  解析

• 7．某种品牌运动服经过两次降价，每件零售价由560元降为315元，已知第二次降价的百分率是第一次的2倍，求第一次降价的百分率．设第一次降价的百分率为x,下面所列的方程中正确的是（　　）

  A．560（1+x）2=315	B．560 （1-x）2=315
  C．560（1-2x）2=315	D．560 （1-x）（1-2x）=315
  组卷：424引用：3难度：0.7

  解析

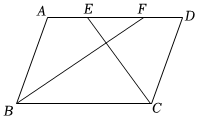• 8．如图，在平行四边形ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，AB=7，EF=3，则BC的长为（　　）

  A．11

  B．12

  C．13

  D．14
  组卷：618引用：5难度：0.5

  解析

三、解答题（本大题共6小题，第21～25题每题6分，第26题10分，共计40分；解答需写出必要的文字说明，演算步骤或证明过程.）

• 25．有两块腰长为20cm的等腰直角△ABC白铁皮．
  
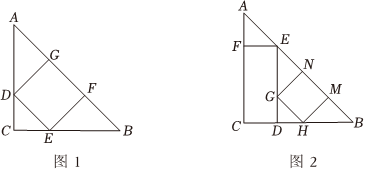
  （1）按图1裁出一块正方形DEFG，四个顶点都在△ABC边上．求裁出正方形的边长．
  （2）按图2裁出面积总和为125cm²的两块矩形铁皮，裁剪过程如下：
  步骤1：在等腰直角△ABC白铁皮上裁下一块长宽不等的矩形CDEF，矩形的四个顶点都在△ABC的边上，留下两块等腰直角三角形零料，分别记为△AEF，△BDE．
  步骤2：取其中一块零料△BDE，从零料上裁下一块正方形GHMN，正方形的四个顶点都在零料边上．
  求裁下的正方形GHMN边长．
  组卷：284引用：1难度：0.5

  解析

• 26．在某探究课《矩形的折叠》中，每个小组分到了相同大小的矩形纸张ABCD，AB=10cm,BC=30cm,各小组通过对该纸张的折叠探究了各种不同的折叠问题．
  

  小组	探究内容	图形
  第一小组	把△ABC沿AC折叠，与△ACD重叠部分记为△ACM．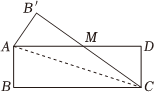
  第二小组	步骤：1：把矩形ABCD沿EF折叠，使得AB与DC重合，点E，F分别为AD，BC上的点． 步骤2：P为边BC上动点（与点B，C不重合），△APB沿AP折叠得到△APB'．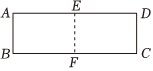
  第三小组	步骤1：把矩形ABCD沿GH折叠，使得AD与BC重合，点G，H分别为AB，DC上的点． 步骤2：P为边BC上动点（与点B，C不重合）， PB沿过点P的一条折痕折叠得到PB'．

  根据以上各小组探究内容，求解下列问题．
  （1）根据第一小组探究内容，求证：△ACM是等腰三角形．
  （2）根据第二小组探究内容，当P，B'，E三点在同一直线上时，求BP的长度．
  （3）根据第三小组探究内容，过点P的折痕使B'落在线段GH上，请直接写出折痕条数与BP长度取值范围的关系．
  组卷：378引用：1难度：0.2

  解析