2022-2023学年上海市浦东新区进才中学高一（下）期末数学试卷

一、填空题（本大题共12题，满分36分，每题3分，请将正确答案直接填写在答题纸相应空格上）

• 1．已知tanx=3，则tan2x=

  ．
  组卷：57引用：1难度：0.7

  解析

• 2．已知复数z=m-3+（m²-9）i（i为虚数单位），若z∈R，则实数m的值为

  ．
  组卷：40引用：1难度：0.7

  解析

• 3．若

  1

  -

  2

  i

  是关于x的实系数方程x²+bx+c=0的一个根，则c=

  ．
  组卷：123引用：4难度：0.8

  解析

• 4．已知数列{a_n}为等比数列，其前n项和为S_n，且a₁=3，q=4，则S₅=

  ．
  组卷：133引用：5难度：0.8

  解析

• 5．已知△ABC的三边a=7，b=5，c=3，则角A的大小是

  ．
  组卷：85引用：1难度：0.8

  解析

• 6．已知向量

  a

  =（2，1），

  b

  =（-1，1），则

  a

  在

  b

  方向上的投影向量为
  组卷：86引用：2难度：0.9

  解析

• 7．已知数列{a_n}的前n项和为S_n=-

  1

  2

  n

  2

  -

  1

  2

  n,数列{b_n}满足b_n=

  2

  a

  n

  ，则

  lim

  n

  →∞

  （b₁+b₂+⋯+b_n）=

  ．
  组卷：83引用：1难度：0.6

  解析

三、解答题（本大题共5题，满分48分，解答要有详细的论证过程与运算步骤，请将解答过程写在答题纸对应位置。）

• 20．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，

  |

  φ

  |

  ≤

  π

  2

  ）

  的图象如图所示．
  （1）求函数f（x）的单调递减区间；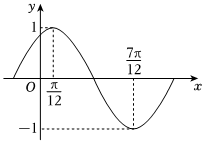
  （2）将函数y=f（x）的图象向右平移

  π

  6

  个单位长度得到曲线C，把C上各点的横坐标伸长到原来的2倍，纵坐标不变，得到的曲线对应的函数记作y=g（x）．
  ①求函数h（x）=f（

  x

  2

  ）g（x）的最小值；
  ②若函数F（x）=g（

  π

  2

  -2x）+mg（x）（m∈R）在（0，4π）内恰有6个零点，求m的值．
  组卷：323引用：3难度：0.4

  解析

• 21．记无穷数列{a_n}的前n项中最大值为M_n，最小值为m_n，令

  b

  n

  =

  M

  n

  +

  m

  n

  2

  ．求：
  （1）若

  a

  n

  =

  2

  n

  -

  3

  n

  ，写出b₁，b₂，b₃，b₄的值；
  （2）设

  a

  n

  =

  2

  n

  -

  λn

  ，若b₃=-3，求λ的值及n≥4时数列{b_n}的前n项和S_n；
  （3）求证：“数列{a_n}是等差数列”的充要条件是“数列{b_n}是等差数列．
  组卷：247引用：3难度：0.3

  解析