2022-2023学年北京市海淀区清华附中九年级（上）月考数学试卷（12月份）

一.选择题（共10题，每题3分）

• 1．在Rt△ABC中，cosA=

  1

  2

  ，那么sinA的值是（　　）

  A． 2 2

  B． 3 2

  C． 3 3

  D． 1 2
  组卷：3138引用：29难度：0.9

  解析

• 2．在Rt△ABC中，∠C=90°，AB=13，AC=5，则sinA的值为（　　）

  A． 5 13

  B． 12 13

  C． 5 12

  D． 12 5
  组卷：4268引用：28难度：0.9

  解析

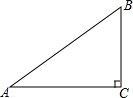• 3．如图，在Rt△ABC中，斜边AB的长为m,∠A=35°，则直角边BC的长是（　　）

  A．msin35°

  B．mcos35°

  C． m sin 35 °

  D． m cos 35 °
  组卷：8011引用：27难度：0.7

  解析

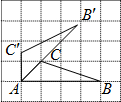• 4．如图，A、B、C三点在正方形网格线的交点处，若将△ABC绕着点A逆时针旋转得到△AC′B′，则tanB′的值为（　　）

  A． 1 2

  B． 1 3

  C． 1 4

  D． 2 4
  组卷：4816引用：142难度：0.9

  解析

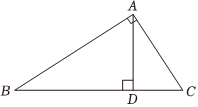• 5．如图，在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，则下列结论不正确的是（　　）

  A． sin B = AD AB

  B． sin B = AC BC

  C． sin B = AD AC

  D． sin B = CD AC
  组卷：7110引用：30难度：0.9

  解析

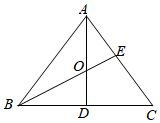• 6．如图，在△ABC中，点O是角平分线AD、BE的交点，若AB=AC=10，BC=12，则tan∠OBD的值是（　　）

  A． 1 2

  B．2

  C． 6 3

  D． 6 4
  组卷：5304引用：15难度：0.5

  解析

• 7．如图，已知△ABC的三个顶点均在格点上，则cosA的值为（　　）
  

  A． 3 3

  B． 5 5

  C． 2 3 3

  D． 2 5 5
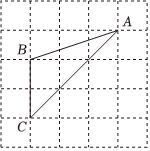  组卷：11291引用：107难度：0.9

  解析

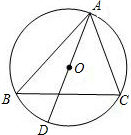• 8．如图，⊙O是△ABC的外接圆，AD是⊙O的直径，若⊙O的半径为

  3

  2

  ，AC=2，则sinB的值是（　　）

  A． 2 3

  B． 3 2

  C． 3 4

  D． 4 3
  组卷：2212引用：83难度：0.7

  解析

三.解答题（共4题，每题10分）

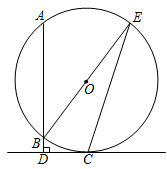• 24．如图，AB是⊙O的弦，C为⊙O上一点，过点C作AB的垂线与AB的延长线交于点D，连接BO并延长，与⊙O交于点E，连接EC，∠ABE=2∠E．
  （1）求证：CD是⊙O的切线；
  （2）若tanE=

  1

  3

  ，BD=1，求AB的长．
  组卷：3117引用：30难度：0.4

  解析

四.新定义（共50分，第（1）（2）（3）问每问10分，第（4）问20分）

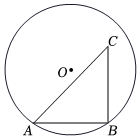• 25．对于点C和给定的⊙O，给出如下定义：若⊙O上存在点B，使点C绕点B旋转90°的对应点A在⊙O上，此时△ABC是以点B为直角顶点的等腰直角三角形，则称点C为⊙O的“等直顶点”．
  若O是坐标原点，⊙O的半径为2，
  （1）在点P（0，0），Q（2，0），R（5，0），S（2

  2

  ，0）中，可以作为⊙O的“等直顶点”的是

  ；
  （2）若点P为⊙O的“等直顶点”，且点P在直线y=x上，求点P的横坐标的取值范围；
  （3）设⊙C的圆心C在x轴上，半径为2，若直线y=x上存在点D，使得半径为1的⊙D上存在点P是⊙C的“等直顶点”，求圆心C的横坐标的取值范围；
  （4）直线y=

  4

  3

  x+4分别和两坐标轴交于E，F两点，若线段EF上的所有点均为⊙O的“等直顶点”，求⊙O的半径的最大值与最小值．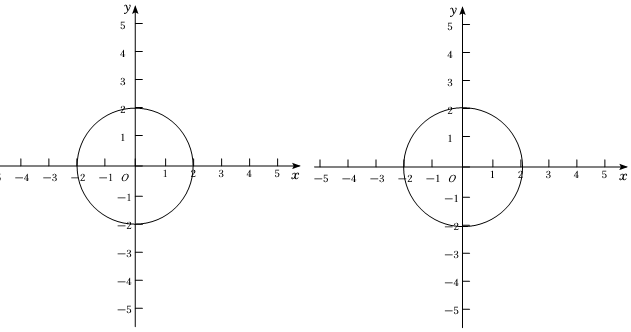
  
  组卷：238引用：2难度：0.1

  解析