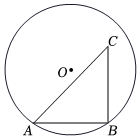
对于点C和给定的⊙O，给出如下定义：若⊙O上存在点B，使点C绕点B旋转90°的对应点A在⊙O上，此时△ABC是以点B为直角顶点的等腰直角三角形，则称点C为⊙O的“等直顶点”．
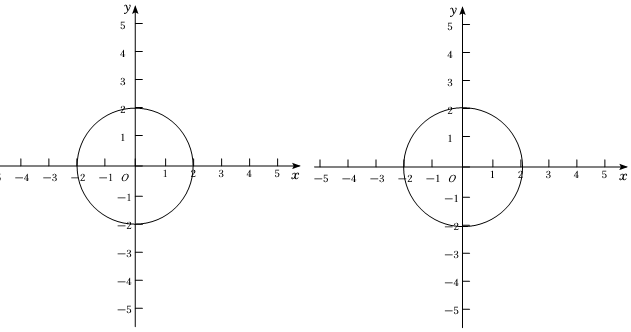
若O是坐标原点，⊙O的半径为2，
（1）在点P（0，0），Q（2，0），R（5，0），S（22，0）中，可以作为⊙O的“等直顶点”的是 Q和SQ和S；
（2）若点P为⊙O的“等直顶点”，且点P在直线y=x上，求点P的横坐标的取值范围；
（3）设⊙C的圆心C在x轴上，半径为2，若直线y=x上存在点D，使得半径为1的⊙D上存在点P是⊙C的“等直顶点”，求圆心C的横坐标的取值范围；
（4）直线y=43x+4分别和两坐标轴交于E，F两点，若线段EF上的所有点均为⊙O的“等直顶点”，求⊙O的半径的最大值与最小值．
2
4
3
【考点】圆的综合题．
【答案】Q和S
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/13 13:0:1组卷：238引用：2难度：0.1
相似题
-
1．等腰三角形AFG中AF=AG，且内接于圆O，D、E为边FG上两点（D在F、E之间），分别延长AD、AE交圆O于B、C两点（如图1），记∠BAF=α，∠AFG=β．
（1）求∠ACB的大小（用α，β表示）；
（2）连接CF，交AB于H（如图2）．若β=45°，且BC×EF=AE×CF．求证：∠AHC=2∠BAC；
（3）在（2）的条件下，取CH中点M，连接OM、GM（如图3），若∠OGM=2α-45°，
①求证：GM∥BC，GM=BC；12
②请直接写出的值．OMMC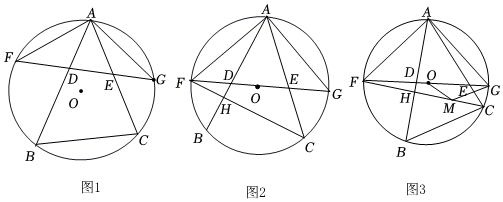
发布：2025/6/7 16:0:2组卷：1490引用：8难度：0.1 -
2．已知，线段AB是⊙O的直径，弦CD⊥AB于点H，点M是优弧CBD上的任意一点，AH=2，CH=4．
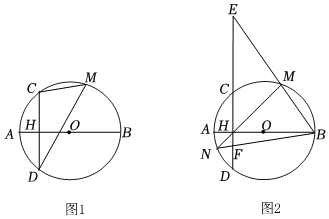
（1）如图1，
①求⊙O的半径；
②求sin∠CMD的值．
（2）如图2，直线BM交直线CD于点E，直线MH交⊙O于点N，连结BN交CD于点F，求HE•FH的值．发布：2025/6/7 7:0:1组卷：476引用：2难度：0.3 -
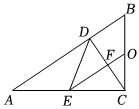3．如图，在Rt△ABC中，∠ACB=90°，过点C作CD⊥AB于点D，O为BC的中点，E是AC的中点，连接OE交CD于点F．
（1）若∠BCD=30°，BC=20，求BD的长；
（2）若∠BCD=30°，求证：以BC为直径的圆与DE相切；
（3）求证：2CE2=AB•EF．发布：2025/6/8 19:30:1组卷：18引用：1难度：0.4
