2022-2023学年广东省广州市真光中学高一（下）质检数学试卷（5月份）

一、单选题

• 1．已知复数z满足z（1+2i）=|4-3i|（其中i为虚数单位），则复数z的虚部为（　　）

  A．-2

  B．-2i

  C．1

  D．i
  组卷：738引用：18难度：0.8

  解析

• 2．已知

  a

  ，

  b

  ，

  c

  是三个平面向量，则下列叙述正确的是（　　）

  A．若 | a | = | b | ，则 a =± b

  B．若 a • b = a • c ，且 a ≠ 0 ，则 b = c

  C．若 a ∥ b ， b ∥ c ，则 a ∥ c

  D．若 a ⊥ b ，则 | a + b | = | a - b |
  组卷：70引用：2难度：0.6

  解析

• 3．已知α，β是平面，m,n是直线，下列命题中不正确的是（　　）

  A．若m∥α，α∩β=n,则m∥n	B．若m∥n,m⊥α，则n⊥α
  C．若m⊥α，m⊥β，则α∥β	D．若m⊥α，m⊂β，则α⊥β
  组卷：245引用：10难度：0.9

  解析

• 4．已知向量

  a

  =（-1，1），

  b

  =（2，x），若

  a

  ∥

  b

  ，则|

  a

  -

  b

  |=（　　）

  A． 3 2

  B．3

  C． 2 2

  D．2
  组卷：616引用：9难度：0.7

  解析

• 5．在△ABC中，内角A，B，C所对的边分别是a,b,c.若（a+c-b）（b+c-a）=4，C=60°，则△ABC的面积是（　　）

  A． 3 4

  B． 3 2

  C． 3

  D． 2 3
  组卷：151引用：3难度：0.7

  解析

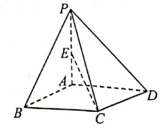• 6．在《九章算术》中，将底面为矩形且有一条侧棱与底面垂直的四棱锥称为“阳马”．如图，四棱锥P-ABCD为阳马，侧棱PA⊥底面ABCD，PA=AB=AD，E为棱PA的中点，则直线CE与平面PAD所成角的正弦值为（　　）

  A． 2 3

  B． 5 3

  C． 3 2

  D． 2 2
  组卷：1120引用：11难度：0.5

  解析

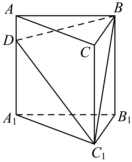• 7．如图，在三棱柱ABC-A₁B₁C₁中，AA₁⊥底面ABC，AB=BC=CA=AA₁，点D是棱AA₁上的点，

  AD

  =

  1

  4

  A

  A

  1

  ，若截面BDC₁分这个棱柱为两部分，则这两部分的体积比为（　　）

  A．1：2

  B．4：5

  C．4：9

  D．5：7
  组卷：485引用：5难度：0.7

  解析

四、解答题

• 21．记△ABC的内角A，B，C的对边分别为a,b,c,已知

  b

  +

  c

  =

  2

  asin

  （

  C

  +

  π

  6

  ）

  ．
  （1）求A；
  （2）设AB的中点为D，若CD=a,且b-c=1，求△ABC的面积．
  组卷：1248引用：8难度：0.6

  解析

• 22．如图，在梯形ABCD中，AD∥BC，BC=2，AB=AD=DC=1，以BD为折痕将△ABD折起，使点A到达点A′的位置，连接A′C．
  
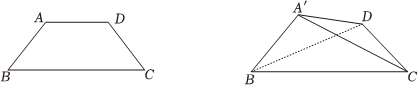
  （1）若点E在线段BC上，使得A′E⊥BD，试确定E的位置，并说明理由；
  （2）当A′C=

  2

  时，求平面A′BC与平面BCD夹角的余弦值．
  组卷：134引用：3难度：0.5

  解析