2022-2023学年广东省深圳高级中学八年级（下）期末数学试卷
发布：2024/6/14 8:0:9
一、选择题。（本大题共10小题，每小题3分，共30分，每个小题有四个选项，其中只有一个是正确的）
-
1．-2023的倒数是（ ）
组卷：225引用：5难度：0.9 -
2．围棋起源于中国，古代称之为“弈”，至今已有4000多年的历史．2017年5月，世界围棋冠军柯洁与人工智能机器人AlphaGo进行围棋人机大战．截取首局对战棋谱中的四个部分，由黑白棋子摆成的图案是中心对称的是（ ）
组卷：2234引用：61难度：0.9 -
3．ChatGPT是人工智能技术驱动的自然语言处理工具，它能够通过理解和学习人类的语言来进行对话．初代GPT语言模型的参数是1.17亿个，而最新模型GPT4的真实参数超过1750亿，1750亿用科学记数法表示为（ ）
组卷：152引用：1难度：0.9 -
4．下列计算中①（ab2）3=ab5；②（3xy2）3=9x3y6；③2x3•3x2=6x5；④（-c）4÷（-c）2=-c2 正确的有（ ）
组卷：322引用：1难度：0.9 -
5．已知关于x的不等式组
无解，则a的取值范围是（ ）3x-a≤0x≥3组卷：684引用：1难度：0.7 -
6．某汽车评测机构对市面上多款新能源汽车的0～100km/h的加速时间和满电续航里程进行了性能评测，评测结果绘制如下，每个点都对应一款新能源汽车的评测数据．已知0～100km/h的加速时间的中位数是m s,满电续航里程的中位数是n km,相应的直线将平面分成了①、②、③、④四个区域（直线不属于任何区域）．欲将最新上市的两款新能源汽车的评测数据对应的点绘制到平面内，若以上两组数据的中位数均保持不变，则这两个点可能分别落在（ ）
组卷：1426引用：5难度：0.6 -
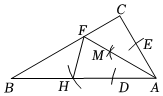7．如图，在Rt△ABC中，∠C=90°，以点A为圆心，任意长为半径作弧，分别交边AB，AC于点D，E，分别以点D，E为圆心，大于DE的长为半径作弧，两弧在∠BAC内相交于点M，作射线AM交BC于点F，以点A为圆心，AF的长为半径作弧，交AB于点H．若∠B=26°，则∠BHF的度数为（ ）12
组卷：557引用：5难度：0.7
三、解答题。（本大题共8题，共55分）
-
22．如图，在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系，直线l1：y=2x-5是河岸，河在l1右侧，l1左侧的A（2，4）是一个河鲜冷藏仓库，B（0，1）是超市．
（1）现计划在河岸l1上建立一座河鲜加工厂C，加工厂C从仓库A进货加工，再运输至超市B，请在图中找出加工厂C的位置，使进出货物的运输路径最短；（仅限在所给网格内作图，不需要说明作图理由）
（2）若河的两岸互相平行，河宽为．5
①在图中画出表示对面河岸的直线l2，并直接写出l2的解析式；
②l2上有一点D，纵坐标为6，l2右侧有一点E（9，3），线段DE是支流（宽度不计），支流有丰富多样的河鲜可以打捞．为支持河鲜产业发展，政府计划垂直于河的两岸造桥，渔民在支流处打捞河鲜后装上货车，运输河鲜到对岸的河鲜冷藏仓库A．请求出l2上的造桥位置F的坐标，以及支流DE上的打捞河鲜位置G的坐标，使运输路径最短．组卷：600引用：2难度：0.4 -
23．【探索发现】
“旋转”是一种重要的图形变换，图形旋转过程中蕴含着众多数学规律，以图形旋转为依托构建的解题方法是解决几何问题的常用方法．如图1，在正方形ABCD中，点E在AD上，点F在CD上，∠EBF=45°．
某同学进行如下探索：
第一步：将△ABE绕点B顺时针旋转90°，得到△CBG，且F、C、G三点共线；
第二步：证明△BEF≌△BGF；
第三步：得到∠AEB和∠FEB的大小关系，以及AE、CF、EF之间的数量关系；
请完成第二步的证明，并写出第三步的结论．
【问题解决】
如图2，在正方形ABCD中，点P在AD上，且不与A、D重合，将△ABP绕点B顺时针旋转，旋转角度小于90°，得到△A'BP'，当P、A′、P′三点共线时，这三点所在直线与CD交于点Q，要求使用无刻度的直尺与圆规找到Q点位置，某同学做法如下：连接AC，与BP交于点O，以O为圆心，OB为半径画圆弧，与CD相交于一点，该点即为所求的点Q．
请证明该同学的做法．（前面【探索发现】中的结论可直接使用，无需再次证明）
【拓展运用】
如图3，在边长为2的正方形ABCD中，点P在AD上，BP与AC交于点O，过点O作BP的垂线，交AB于点M，交CD于点N，设AP+AB=x（2≤x≤4），AM=y,直接写出y关于x的函数表达式．
组卷：846引用：1难度：0.5
