2023-2024学年辽宁省沈阳120中高二（上）期初数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。

• 1．已知

  {

  a

  ，

  b

  ，

  c

  }

  是空间的一组基底，则可以与向量

  p

  =

  a

  +

  b

  ，

  q

  =

  a

  -

  b

  构成基底的向量（　　）

  A． a

  B． b

  C． a + b

  D． a + 2 c
  组卷：147引用：2难度：0.8

  解析

• 2．下列函数中，最小正周期为2π的奇函数是（　　）

  A．y=tanx	B．y=cosx
  C．y=sin（x+3π）	D．y=sin2x
  组卷：106引用：3难度：0.8

  解析

• 3．设m,n是两条不同的直线，α，β是两个不同的平面，则下列结论中正确的是（　　）

  A．若m∥n,n∥α，则m∥α	B．若m∥α，n∥α，则m∥n
  C．若m∥n,m∥α，n∥β，则α∥β	D．若m⊥α，n⊥β，α⊥β，则m⊥n
  组卷：83引用：6难度：0.7

  解析

• 4．函数f（x）=

  sin

  （

  πx

  ）

  x

  2

  的图象大致为（　　）

  A．	B．
  C．	D．
  组卷：102引用：6难度：0.8

  解析

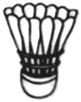• 5．羽毛球运动是一项全民喜爱的体育运动，标准的羽毛球由16根羽毛固定在球托上，测得每根羽毛在球托之外的长为8cm,球托之外由羽毛围成的部分可看成一个圆台的侧面，测得顶部所围成圆的直径是6cm,底部所围成圆的直径是2cm,据此可估算球托之外羽毛球所在曲面的展开图的圆心角为（　　）

  A． 2 π 3

  B． 3 π 4

  C． π 2

  D． π 3
  组卷：97引用：3难度：0.7

  解析

• 6．已知函数

  f

  （

  x

  ）

  =

  xsin

  （

  ωx

  +

  π

  4

  ）

  ，

  ∀

  x

  1

  ，

  x

  2

  ∈

  （

  π

  2

  ，

  5

  π

  6

  ）

  ，且x₁＜x₂，都有x₂f（x₁）-x₁f（x₂）＞0，则ω的取值范围可能是（　　）

  A． [ 1 2 ， 3 2 ]

  B． [ 1 2 ， 5 4 ]

  C． [ 3 2 ， 9 4 ]

  D． [ 0 ， 1 2 ]
  组卷：213引用：4难度：0.5

  解析

• 7．已知四棱锥P-ABCD的底面ABCD是边长为2的正方形，且∠PAB=90°．若四棱锥P-ABCD的五个顶点在同一球面上，已知棱PA最大值为

  2

  5

  ，则四棱锥P-ABCD的外接球体积为（　　）

  A．24π

  B． 8 6 π

  C．28π

  D． 28 7 3 π
  组卷：156引用：3难度：0.5

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

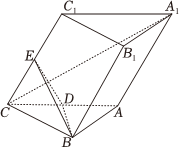• 21．如图，在三棱柱 ABC-A₁B₁C₁ 中，底面是边长为2的等边三角形，CC₁=2，D，E分别是线段AC，CC₁的中点，C₁在平面ABC内的射影为D．
  （1）求证：A₁C⊥平面BDE；
  （2）若点F为线段 B₁C₁上的动点（不包括端点），求锐二面角F-BD-E的余弦值的取值范围．
  组卷：179引用：8难度：0.5

  解析

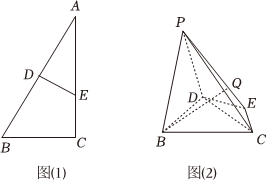• 22．如图（1）所示，在△ABC中，AB=4

  3

  ，BC=2

  3

  ，∠B=60°，DE垂直平分AB．现将△ADE沿DE折起，使得二面角A-DE-B大小为60°，得到如图（2）所示的空间几何体（折叠后点A记作点P）
  （1）求点D到面PEC的距离；
  （2）求四棱锥P-BCED外接球的体积；
  （3）点Q为一动点，满足

  PQ

  =

  λ

  PE

  （0＜λ＜1），当直线BQ与平面PEC所成角最大时，试确定点Q的位置．
  组卷：57引用：2难度：0.5

  解析