当前位置：试卷中心 > 试卷详情

2022-2023学年山西省临汾市襄汾县八年级（上）期中数学试卷

发布：2024/8/29 4:0:8

一、选择题(本大题共10个小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑)

1．下列实数
31
7
，3.14-π，3.14259，
8
，-
3
27
，1² 中无理数有（　　）
A．2个 B．3个 C．4个 D．5个
组卷：126引用：4难度：0.7
解析
2．下列计算中正确的是（　　）
A．a³•a³=a⁹ B．（-2a）³=-8a³
C．a¹⁰÷（-a²）³=a⁴ D．（-a+2）（-a-2）=a²+4
组卷：683引用：12难度：0.7
解析
3．下列命题是假命题的是（　　）
A．所有的实数都可用数轴上的点表示
B．同位角相等，两直线平行
C．无理数包括正无理数，0，负无理数
D．两点之间，线段最短
组卷：52引用：4难度：0.7
解析
4．等腰三角形顶角度数比一个底角度数的2倍多20°，则这个底角的度数是（　　）
A．30° B．40° C．50° D．60°
组卷：1647引用：10难度：0.7
解析
5．若2⁴×2²=2^m，则m的值为（　　）
A．8 B．6 C．5 D．2
组卷：2439引用：4难度：0.8
解析
6．如图，在△ABC和△DEF中，点A，E，B，D在同一直线上，AC∥DF，AC=DF，只添加一个条件，能判定△ABC≌△DEF的是（　　）
A．BC=DE B．AE=DB C．∠A=∠DEF D．∠ABC=∠D
组卷：3209引用：36难度：0.9
解析
7．下面各式从左到右的变形，属于因式分解的是（　　）
A．x²-x-l=x （x-1）-1 B．x²-1=（x-1）²
C．x²-x-6=（x-3）（x+2） D．x （x-1）=x²-x
组卷：106引用：1难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共8个小题，共75分。解答应写出文字说明、证明过程或演算步骤）

22．阅读与思考
请仔细阅读下面的材料并完成相应的问题．
阅读材料
问题：若（8-x）（x-6）=-3，求（8-x）²+（x-6）²的值．
解：设（8-x）=a,（x-6）=b,
则（8-x）（x-6）=ab=-3，a+b=8-x+x-6=2，
∴（8-x）²+（x-6）²=a²+b²=（a+b）²-2ab=2²-2×（-3）=10；
请仿照上例解决下面的问题：
问题发现：
（1）若x满足（3-x）（x-2）=-10，求（3-x）²+（x-2）²的值．
类比探究：
（2）若x满足（2022-x）²+（x-2023）²=2021，求（2022-x）（x-2023）的值．
拓展延伸：
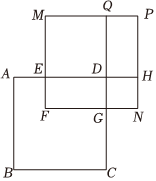
（3）如图，正方形ABCD和正方形和MFNP重叠，其重叠部分是一个长方形，分别延长AD、CD，交NP和MP于H、Q两点，构成的四边形NGDH和MEDQ都是正方形，四边形PQDH是长方形．若正方形ABCD的边长为x,AE=10，CG=20，长方形EFGD的面积为200．则正方形MFNP的面积为
（结果必须是一个具体数值）．
组卷：65引用：2难度：0.5
解析
23．综合实践
在学习全等三角形的知识时，数学兴趣小组发现这样一个模型：它是由两个共顶点且顶角相等的等腰三角形构成的，在相对位置变化的同时，始终存在一对全等三角形．兴趣小组成员经过研讨给出定义：如果两个等腰三角形的顶角相等，且顶角的顶点互相重合，则称此图形为“手拉手全等模型”．因为顶点相连的四条边，可以形象地看作两双手，所以通常称为“手拉手模型”，如图1，△ABC与△ADE都是等腰三角形，其中∠BAC=∠DAE，则△ABD≌△ACE（SAS）．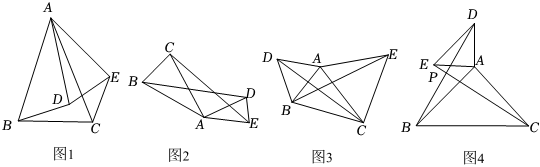

[初步把握]如图2，△ABC与△ADE都是等腰三角形，AB=AC，AD=AE，且∠BAC=∠DAE，则有
≌
．
[深入研究]如图3，已知△ABC，以AB、AC为边分别向外作等边△ABD和等边△ACE，并连接BE，CD，求证：BE=CD．
[拓展延伸]如图4，在两个等腰直角三角形△ABC和△ADE中，AB=AC，AE=AD，∠BAC=∠DAE=90°，连接BD，CE，交于点P，请判断BD和CE的关系，并说明理由．
组卷：2247引用：11难度：0.3
解析