2022-2023学年上海市浦东新区南汇中学高二（下）期中数学试卷

一、填空题（每小题3分，共12题，共36分）

• 1．直线x-

  3

  y+1=0的倾斜角大小为

  ．
  组卷：60引用：5难度：0.9

  解析

• 2．抛物线y²=-x的准线方程是

  ．
  组卷：109引用：5难度：0.7

  解析

• 3．双曲线

  x

  2

  2

  -

  y

  2

  =

  1

  的焦距为

  ．
  组卷：87引用：8难度：0.8

  解析

• 4．椭圆

  x

  2

  9

  +

  y

  2

  5

  =

  1

  的离心率为

  ．
  组卷：303引用：4难度：0.7

  解析

• 5．函数f（x）=x²在区间[2，4]上的平均变化率等于

  ．
  组卷：231引用：6难度：0.8

  解析

• 6．两直线3x-y+1=0，x-2y+3=0的夹角的大小为

  ．（用反三角函数形式表示）
  组卷：43引用：1难度：0.6

  解析

• 7．若直线l经过点（1，3），且与圆x²+y²=10相切，则直线l的方程是

  ．
  组卷：310引用：4难度：0.7

  解析

三、解答题（共5题，总计52分）

• 20．已知曲线C的方程是（1-a²）x²+y²+a²-1=0，其中a＞0，a≠1，直线l的方程是

  y

  =

  2

  2

  x

  -

  a

  ．
  （1）请根据a的不同取值，判断曲线C是何种圆锥曲线；
  （2）若直线l交曲线C于两点M，N，且线段MN中点的横坐标是-2，求a的值；
  （3）若

  a

  =

  2

  ，试问曲线C上是否存在不同的两点A，B，使得A，B关于直线l对称，并说明理由．
  组卷：58引用：1难度：0.4

  解析

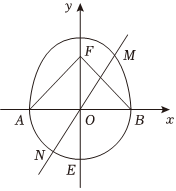• 21．如图，已知半圆C₁：x²+y²=b²（y≤0）与x轴交于A、B两点，与y轴交于E点，半椭圆C₂：

  y

  2

  a

  2

  +

  x

  2

  b

  2

  =1（y＞0，a＞b＞0）的上焦点为F，并且△ABF是面积为

  3

  的等边三角形，将由C₁、C₂构成的曲线，记为“Γ”．
  （1）求实数a、b的值；
  （2）直线l：y=

  2

  x与曲线Γ交于M、N两点，在曲线Γ上再取两点S、T（S、T分别在直线l两侧），使得这四个点形成的四边形MSNT的面积最大，求此最大面积；
  （3）设点K（0，t）（t∈R），P是曲线Γ上任意一点，求|PK|的最小值．
  组卷：423引用：7难度：0.2

  解析