2022-2023学年贵州省铜仁市八年级（下）期末数学试卷
发布：2024/8/1 8:0:9
一、选择题：共12道题，每小题3分，共36分.
-
1．国家级非物质文化遗产松桃苗绣，构图夸张浪漫，颜色素净淡雅，以花鸟虫鱼，飞禽走兽等为题材，体现苗族人民向往自由与和平的精神世界，如所示四幅苗绣图样中，是中心对称图形的是（ ）
组卷：21引用：1难度：0.9 -
2．下列各数化简后为负数的是（ ）
组卷：80引用：2难度：0.6 -
3．铜仁市某校为响应国家“双减”政策（减轻学生作业负担、减轻校外培训负担），落实教育部“五项管理”（作业、睡眠、手机、读物、体质）工作要求，以便根据学校学生实际情况制定相应措施，随机抽取50名学生进行问卷调查，并将调查结果制成不完整的统计表（如表）．则m的值是（ ）
作业时间频数分布组别 作业时间（单位：分钟） 频数 A 60＜t≤70 8 B 70＜t≤80 17 C 80＜t≤90 m D t＞90 5 组卷：161引用：2难度：0.5 -
4．估计
的结果应在（ ）（27+6）×13组卷：30引用：2难度：0.7 -
5．已知一次函数y=（m+1）x-2，y的值随x的增大而减小，则点P（-m,m）所在象限为（ ）
组卷：343引用：3难度：0.5 -
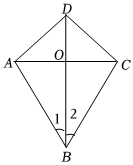6．等腰三角形“三线合一”是应用特别广泛的一个重要模型，小明对与其相关的习题解题热情高涨．如图，四边形ABCD的对角线AC、BD交于点O，小明根据所给条件依次进行了探究，在其得出的四个命题中，假命题的是（ ）组卷：93引用：3难度：0.5 -
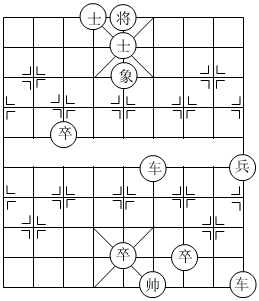7．中国象棋文化历史久远，雅俗共赏，具有广泛的参与度．象棋残局是象棋的基础，《七星聚会》素有“残局之王”的称谓，深受广大棋迷喜爱．如图就是残局《七星聚会》．如果建立平面直角坐标系，使“帥”位于点（-1，-2），“象”位于点（-2，5），那么“兵”在同一坐标系下的坐标是（ ）组卷：212引用：3难度：0.5 -
8．成书于大约公元前1世纪的《周髀算经》是中国现存最早的一部数学典籍，里面记载的勾股定理的公式与证明相传是在西周由商高发现，故又称之为商高定理．观察下列勾股数：3，4，5；5，12，13；7，24，25；…，这类勾股数的特点是：勾为奇数，弦与股相差为1；古希腊哲学家柏拉图（公元前427年—公元前347年）研究了勾为2m（m≥3，m为正整数），弦与股相差为2的一类勾股数，如：6，8，10；8，15，17；…，若此类勾股数的勾为12，则其股为（ ）组卷：232引用：6难度：0.5
三、解答题：共9道题，17，18，19，20，21，22每题10分，23，24每题12分，25题14分，共98分.
-
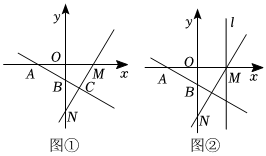24．如图①，在平面直角坐标系中，直线MN交x轴正半轴于点M，交y轴负半轴于点N（0，-6），∠ONM=30°，作线段MN的垂直平分线交x轴于点A，交y轴于点B，交MN于点C．
（1）求AM的长；
（2）如图②，过点M作y轴的平行线l,在l上是否存在一点P，使得△PAN的周长最小？若存在，求出点P的坐标；若不存在，说明理由．组卷：116引用：2难度：0.5 -
25．（1）阅读理解
由两个顶角相等且有公共顶角顶点的特殊多边形组成的图形，如果把它们的底角顶点连接起来，则在相对位置变化的过程中，始终存在一对全等三角形，我们把这种模型称为“手拉手模型”．在如图①所示的“手拉手”图形中，小白发现若∠BAC=∠DAE，AB=AC，AD=AE，则△ABD≌△ACE，请证明他的发现；
（2）问题解决
如图②，∠BAC=∠DAE=90°，AB=AC，AD=AE，试探索线段CD，BD，DE之间满足的等量关系，并证明；
（3）拓展探究
如图③，△ABC和△DEC是拥有公共顶点C的两个等边三角形，M点、N点、F点分别是DE、AB、AE的中点．当AD=10时，请直接写出MN的长．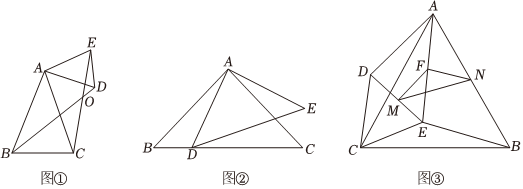
组卷：363引用：2难度：0.5
