2023年河南省焦作市武陟县中考数学三模试卷
发布：2024/6/23 8:0:10
一、选择题（每小题3分，共30分）下列各小题均有四个答案，其中只有一个是正确的
-
1．如果温度上升2℃，记作+2℃，那么温度下降1℃记作（ ）
组卷：333引用：2难度：0.5 -
2．为加快中心城市建设，市政府拟建多个城市休闲文化广场或公园，已知某正方形公园的边长为4×102m,其面积用科学记数法表示为1.6×10n，则n为（ ）
组卷：53引用：2难度：0.8 -
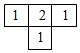3．如图是由5个立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上的小立方块的个数，则这个几何体的主视图是（ ）组卷：1173引用：7难度：0.6 -
4．如图，在△ABC中，∠B=50°，∠C=70°，直线DE经过点A，∠DAB=50°，则∠EAC的度数是（ ）组卷：688引用：6难度：0.7 -
5．下列运算正确的是（ ）
组卷：91引用：1难度：0.7 -
6．第十一届中国（郑州）国际园林博览园坐落于郑州航空港经济综合实验区，共有园博园、双鹤湖中央公园、苑陵故城遗址公园三个园区，因园区规模较大，一天只能游玩这三个园区中的一个，小明和小亮随机选择一个园区进入，则小明和小亮选择同一个园区进行游玩的概率为（ ）
组卷：36引用：1难度：0.5 -
7．已知x=2是关于x的方程x2-（m+4）x+4m=0的一个实数根，且该方程的两实数根恰是等腰△ABC的两条边长，则△ABC的周长为（ ）
组卷：598引用：6难度：0.5
三、解答题（本大题共8个小题，满分75分）
-
22．如图，在以AB为直径的⊙O中，AC切⊙O于点A，且AC=AB，连接BC，交⊙O于点D，作射线CO交⊙O于点E．
（1）作AM⊥CE于点M，交BC于点N，交⊙O于点F，连接BF（尺规作图，保留作图痕迹，不写作法）；
（2）在（1）的条件下，
①求证：△ACM≌△BAF；
②若AF=12，求BD的长．组卷：59引用：1难度：0.5 -
23．综合与实践综合与实践课上，数学研究小组以“最短距离”为主题开展数学活动．发现问题，如图1，在△ABC中，∠ACB=90°，D为边AB上的一个动点，连接CD，数学研究小组的开元同学发现：线段CD的长度是一个变量，随着点D位置变化而变化，影响线段长度的因素有多个．
（1）提出问题，当AC=5，BC=12，则CD长度的最小值为 ；
（2）探究规律，如图2，在矩形ABCD中，顺次连接边CD，AD，AB，BC上的点E，F，G，H，得到四边形EFGH，再连接F、H，若FH∥AB，AB=6，BC=8，则四边形EFGH的面积是否为定值？若是，求出该定值；若不是，请说明理由；
（3）实践应用，农为邦本，本固邦宁，习近平总书记多次在不同场合发表重要讲话、作出重要部署，始终坚持把解决好“三农”问题作为全党工作的重中之重．某农科所基地规划一块小麦试验田，并将小麦试验田划分为四个区域．如图3，按照设计图的思路，小麦试验田的平面示意图为四边形ABCD，∠ADC=90°，点O在四边形ABCD的对角线AC上，且满足OD=100m,CD=200m,OB∥AD，∠OBC=30°．计划在小麦试验田△ABC区域试种新品种“豫麦23号”，由于小麦试验田占地有限，探究△ABC的面积是否存在最小值．若存在，直接写出△ABC面积的最小值；若不存在，请说明理由．
组卷：126引用：1难度：0.5
