2023-2024学年黑龙江省哈尔滨一中高二（上）期中数学试卷

一、单选题（每题5分，共40分）

• 1．直线

  3

  x-y+1=0的倾斜角为（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  组卷：1930引用：47难度：0.9

  解析

• 2．已知

  a

  =（3，0，2），

  b

  =（2，x,1），

  c

  =（-2，4，y），（

  a

  -

  b

  ）∥

  c

  ，则x+y=（　　）

  A．2

  B． 3 2

  C．1

  D．0
  组卷：63引用：3难度：0.8

  解析

• 3．下列关于空间向量的说法中正确的是（　　）

  A．方向相反的两个向量是相反向量

  B．空间中任意两个单位向量必相等

  C．若向量 AB ， CD 满足 | AB | ＞ | CD | ，则 AB ＞ CD

  D．相等向量其方向必相同
  组卷：313引用：5难度：0.8

  解析

• 4．直线l₁：x+ay+2a=0和直线l₂：（a-2）x+3y=0互相垂直，则实数a的值为（　　）

  A．a=-3

  B． a = 1 2

  C．a=1或a=3

  D．a=-1或a=3
  组卷：78引用：3难度：0.7

  解析

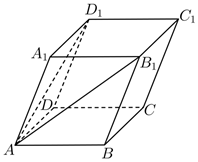• 5．如图，在平行六面体ABCD-A₁B₁C₁D₁中，AA₁=AD=AB=2，∠BAD=

  π

  2

  ，∠BAA₁=∠A₁AD=

  π

  3

  ，则

  A

  B

  1

  •

  A

  D

  1

  =（　　）

  A．12

  B．8

  C．6

  D．4
  组卷：100引用：10难度：0.7

  解析

• 6．古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名．他发现：“平面内到两个定点A，B的距离之比为定值λ（λ≠1）的点的轨迹是圆”．后来，人们将这个圆以他的名字命名，称为阿波罗尼斯圆，简称阿氏圆在平面直角坐标系xOy中，A（-2，0），B（4，0），点P满足

  |

  PA

  |

  |

  PB

  |

  =

  1

  2

  ．则点P的轨迹所包围的图形的面积等于（　　）

  A．4π

  B．8π

  C．12π

  D．16π
  组卷：187引用：4难度：0.8

  解析

• 7．已知M，N分别是曲线C₁：x²+y²-4x-4y+7=0，C₂：x²+y²-2x=0上的两个动点，P为直线x+y+1=0上的一个动点，则|PM|+|PN|的最小值为（　　）

  A． 2

  B． 3

  C．2

  D．3
  组卷：946引用：8难度：0.5

  解析

四、解答（17题10分，18-22题每题12分，共70分）

• 21．在四棱锥P-ABCD中，平面PAD⊥平面ABCD，PA=PD，O为AD的中点．
  （1）求证：PO⊥BC；
  （2）若AB∥CD，AB=8，AD=DC=CB=4，

  PO

  =

  2

  7

  ，点E在棱PB上，直线AE与平面ABCD所成角为

  π

  6

  ，求点E到平面PCD的距离．
  组卷：176引用：4难度：0.4

  解析

• 22．已知线段RQ的端点Q的坐标是（4，3），端点R在圆（x+2）²+（y+3）²=16上运动，线段RQ中点的轨迹为曲线C．
  （1）求曲线C的方程；
  （2）直线l经过坐标原点，且不与y轴重合，直线l与曲线C相交于M（x₁，y₁），N（x₂，y₂）两点，求证：

  1

  x

  1

  +

  1

  x

  2

  为定值；
  （3）已知过点P（m,-3）（m＞0）有且只有一条直线与圆x²+y²=10相切，过点P作两条倾斜角互补的直线与圆x²+y²=10交于E，F两点，求E，F两点间距离的最大值．
  组卷：114引用：3难度：0.4

  解析