2022-2023学年北京市顺义区牛栏山一中高一(下)月考数学试卷(6月份)
发布:2024/5/26 8:0:9
一、选择题(本大题共10小题,每小题4分,共40分,四个选项中只有一是符合题目)
-
1.已知正四棱锥的底面边长为2,高为3,则它的体积为( )
组卷:471引用:4难度:0.8 -
2.复数z=i(1+i)(i是虚数单位)在复平面内所对应点的坐标为( )
组卷:17引用:9难度:0.9 -
3.将函数f(x)=sin2x的图象向右平移φ个单位长度后得到函数
的图象,则φ的最小值是( )f(x)=sin(2x-π3)组卷:321引用:3难度:0.8 -
4.已知直线m和平面α,β,则下列四个命题中正确的是( )
组卷:152引用:10难度:0.7 -
5.在△ABC中,
,则∠A=( )3asinB=3bcosA组卷:689引用:4难度:0.8 -
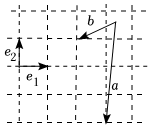 6.向量,a,b,e在正方形网格中的位置如图所示,若e2a=λ-b+μe1(λ,μ∈R),则e2=( )λμ组卷:395引用:8难度:0.7
6.向量,a,b,e在正方形网格中的位置如图所示,若e2a=λ-b+μe1(λ,μ∈R),则e2=( )λμ组卷:395引用:8难度:0.7
三、解答题(本大题共6小题,共85分,解答应写出文字说明过程或演算步骤.)
-
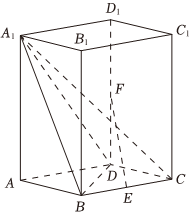 19.如图,在直棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,AB=2,∠BAD=60°,AA1=a,E,F分别是棱BC,DD1的中点.
19.如图,在直棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,AB=2,∠BAD=60°,AA1=a,E,F分别是棱BC,DD1的中点.
(Ⅰ)求证:BD⊥A1C;
(Ⅱ)求证:EF∥平面A1BD;
(Ⅲ)若平面A1BC⊥平面A1DC,求a的值.组卷:331引用:1难度:0.4 -
20.若点(x0,y0)在函数f(x)的图象上,且满足y0•f(y0)≥0,则称x0是f(x)的ξ点.函数f(x)的所有ξ点构成的集合称为f(x)的ξ集.
(Ⅰ)判断是否是函数f(x)=tanx的ξ点,并说明理由;2π3
(Ⅱ)若函数f(x)=sin(πx),求f(x)的ξ集;
(Ⅲ)若定义域为R的连续函数f(x)的ξ集D是实数集的真子集,求证:{x|f(x)=0}≠∅.组卷:8引用:1难度:0.5


