2023-2024学年重庆十一中教育集团高二（上）期中数学试卷

一、单选题（本大题共8小题，每小题5分，共40分）

• 1．已知两点A（-1，2），B（3，4），则直线AB的斜率为（　　）

  A．2

  B． - 1 2

  C． 1 2

  D．-2
  组卷：216引用：5难度：0.8

  解析

• 2．在棱长为1的正四面体ABCD中，直线AD与BC是（　　）

  A．平行直线	B．相交直线
  C．异面直线	D．无法判断位置关系
  组卷：54引用：1难度：0.8

  解析

• 3．已知l,m表示两条不同的直线，α表示平面，则下列说法正确的是（　　）

  A．若l⊥α，m⊂α，则l⊥m	B．若l⊥m,m⊂α，则l⊥α
  C．若l∥m,m⊂α，则l∥α	D．若l∥α，m⊂α，则l∥m
  组卷：364引用：13难度：0.9

  解析

• 4．已知双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的两条渐近线均与圆（x-a）²+y²=

  b

  2

  4

  相切，则双曲线C的离心率为（　　）

  A． 3

  B．2

  C．3

  D．4
  组卷：244引用：8难度：0.7

  解析

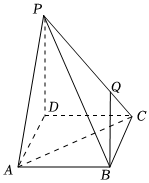• 5．如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC=4，Q为PC上一点，且PQ=3QC，则异面直线AC与BQ所成的角的大小为（　　）

  A． π 6

  B． π 3

  C． 5 π 6

  D． 2 π 3
  组卷：153引用：4难度：0.7

  解析

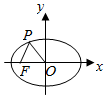• 6．如图，已知椭圆C的中心为原点O，F（-2

  5

  ，0）为C的左焦点，P为C上一点，满足|OP|=|OF|且|PF|=4，则椭圆C的方程为（　　）

  A． x 2 25 + y 2 5 =1	B． x 2 36 + y 2 16 =1
  C． x 2 30 + y 2 10 =1	D． x 2 45 + y 2 25 =1
  组卷：774引用：17难度：0.9

  解析

• 7．已知实数x,y满足方程（x-2）²+y²=3．则

  y

  x

  的最大值和最小值分别为（　　）

  A． 2 3 ，- 2 3

  B． 3 ，- 3

  C． 3 3 ，- 3 3

  D． 2 3 3 ， - 2 3 3
  组卷：103引用：4难度：0.6

  解析

四、解答题（本大题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤）

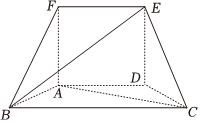• 21．如图，正方形ADEF所在平面和等腰梯形ABCD所在平面相互垂直，已知BC=4，AB=AD=2．
  （1）求证：AC⊥BF；
  （2）在线段BE上是否存在一点P，使得平面PAC⊥平面BCEF？若存在，求出

  |

  PE

  |

  |

  BP

  |

  的值；若不存在，请说明理由．
  组卷：92引用：1难度：0.7

  解析

• 22．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的离心率为

  3

  2

  ，点A为椭圆C的右顶点，点B为椭圆上一动点，O为坐标原点，若△OAB面积的最大值为1．
  （1）求椭圆C的方程；
  （2）设直线l：y=kx+m与椭圆C交于M，N两点，O为坐标原点，若

  k

  OM

  •

  k

  ON

  =

  5

  4

  ，求△MON面积的最大值．
  组卷：137引用：1难度：0.3

  解析