当前位置：试卷中心 > 试卷详情

2023-2024学年湖南省衡阳市衡阳县九年级（上）五科联赛数学试卷

发布：2024/9/3 4:0:8

一、选择题（本大题共15个小题，每小题3分，共计45分）

1．下列单项式中，a²b³的同类项是（　　）
A．a³b² B．3a²b³ C．a²b D．ab³
组卷：2164引用：32难度：0.8
解析
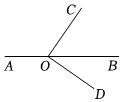2．如图，点O在直线AB上，∠COD=75°．若∠AOC=135°，则∠BOD的大小为（　　）
A．15° B．20° C．30° D．45°
组卷：361引用：2难度：0.6
解析
3．已知43²=1849，44²=1936，45²=2025，46²=2116，若n为整数，且
n
＜
2023
.
2
＜
n
+
1
．则n的值为（　　）
A．43 B．44 C．45 D．46
组卷：96引用：1难度：0.6
解析
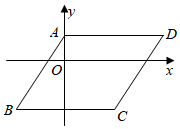4．如图，▱ABCD的顶点A，B，C的坐标分别是（0，1），（-2，-2），（2，-2），则顶点D的坐标是（　　）
A．（-4，1） B．（4，-2） C．（4，1） D．（2，1）
组卷：2573引用：18难度：0.6
解析
5．若点A（-5，y₁），B（1，y₂），C（5，y₃）都在反比例函数y=-
5
x
的图象上，则y₁，y₂，y₃的大小关系是（　　）
A．y₁＜y₂＜y₃ B．y₂＜y₃＜y₁ C．y₁＜y₃＜y₂ D．y₃＜y₁＜y₂
组卷：1977引用：24难度：0.6
解析
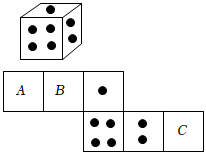6．一个骰子相对两面的点数之和为7，它的展开图如图，下列判断正确的是（　　）
A．B代表 B．A代表 C．C代表 D．B代表
组卷：436引用：14难度：0.7
解析
7．学校招募运动会广播员，从两名男生和两名女生共四名候选人中随机选取两人，则两人恰好是一男一女的概率是（　　）
A．
1
3
B．
1
2
C．
2
3
D．
3
4
组卷：1537引用：15难度：0.5
解析
8．我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式，此公式与古希腊几何学家海伦提出的公式如出一辙，即三角形的三边长分别为a,b,c,记p=
a
+
b
+
c
2
，则其面积S=
p
（
p
-
a
）
（
p
-
b
）
（
p
-
c
）
．这个公式也被称为海伦-秦九韶公式．若p=5，c=4，则此三角形面积的最大值为（　　）
A．
5
B．4 C．2
5
D．5
组卷：3618引用：13难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共6个小题，共计60分）

25．“田忌赛马”的故事闪烁着我国古代先贤的智慧光芒．该故事的大意是：齐王有上、中、下三匹马A₁，B₁，C₁，田忌也有上、中、下三匹马A₂，B₂，C₂，且这六匹马在比赛中的胜负可用不等式表示如下：A₁＞A₂＞B₁＞B₂＞C₁＞C₂（注：A＞B表示A马与B马比赛，A马获胜）．一天，齐王找田忌赛马，约定：每匹马都出场比赛一局，共赛三局，胜两局者获得整场比赛的胜利．面对劣势，田忌事先了解到齐王三局比赛的“出马”顺序为上马、中马、下马，并采用孙膑的策略：分别用下马、上马、中马与齐王的上马、中马、下马比赛，即借助对阵（C₂A₁，A₂B₁，B₂C₁）获得了整场比赛的胜利，创造了以弱胜强的经典案例．
假设齐王事先不打探田忌的“出马”情况，试回答以下问题：
（1）如果田忌事先只打探到齐王首局将出“上马”，他首局应出哪种马才可能获得整场比赛的胜利？并求其获胜的概率；
（2）如果田忌事先无法打探到齐王各局的“出马”情况，他是否必败无疑？若是，请说明理由；若不是，请列出田忌获得整场比赛胜利的所有对阵情况，并求其获胜的概率．
组卷：1932引用：8难度：0.6
解析
26．如果一个自然数M的个位数字不为0，且能分解成A×B，其中A与B都是两位数，A与B的十位数字相同，个位数字之和为10，则称数M为“合和数”，并把数M分解成M=A×B的过程，称为“合分解”．
例如∵609=21×29，21和29的十位数字相同，个位数字之和为10，
∴609是“合和数”．
又如∵234=18×13，18和13的十位数字相同，但个位数字之和不等于10，
∴234不是“合和数”．
（1）判断168，621是否是“合和数”？并说明理由；
（2）把一个四位“合和数”M进行“合分解”，即M=A×B．A的各个数位数字之和与B的各个数位数字之和的和记为P（M）；A的各个数位数字之和与B的各个数位数字之和的差的绝对值记为Q（M）．令G（M）=
P
（
M
）
Q
（
M
）
，当G（M）能被4整除时，求出所有满足条件的M．
组卷：2270引用：11难度：0.5
解析