当前位置：试卷中心 > 试卷详情

2022-2023学年四川省广安二中高二（上）期中数学试卷（理科）

发布：2024/9/6 11:0:13

一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1．抛物线y=4x²的焦点坐标是（　　）
A．（0，1） B．（0，2） C．（0，4） D．（0，
1
16
）
组卷：424引用：7难度：0.9
解析
2．已知命题p：∃x＜-1，2^x-x-1＜0，则¬p为（　　）
A．∀x≥-1，2^x-x-1≥0 B．∀x＜-1，2^x-x-1≥0
C．∃x＜-1，2^x-x-1≥0 D．∃x≥-1，2^x-x-1≥0
组卷：3引用：4难度：0.8
解析
3．设a∈R，则“a=1”是“直线l₁：ax+2y-1=0直线l₂：x+（a+1）y+3=0平行”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分又不必要条件
组卷：74引用：5难度：0.9
解析
4．曲线
x
2
25
+
y
2
9
=1与曲线
x
2
25
-
k
+
y
2
9
-
k
=1（k＜9）的（　　）
A．长轴长相等 B．短轴长相等 C．离心率相等 D．焦距相等
组卷：2991引用：98难度：0.9
解析
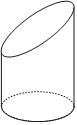5．美学四大构件是：史诗、音乐、造型（绘画、建筑等）和数学．素描是学习绘画的必要一步，它包括明暗素描和结构素描，而学习几何体结构素描是学习素描的重要一步．某同学在画切面圆柱体（用与圆柱底面不平行的平面去截圆柱，底面与截面之间的部分叫做切面圆柱体，原圆柱的母线被截面所截剩余的部分称为切面圆柱体的母线）的过程中，发现“切面”是一个椭圆，若切面圆柱体的最长母线与最短母线所确定的平面截切面圆柱体得到的截面图形是一个底角为60°的直角梯形，设圆柱半径r=1，则该椭圆的焦距为（　　）
A．
2
3
3
B．
3
3
C．
3
2
D．
1
3
组卷：21引用：2难度：0.5
解析
6．圆C与直线x-y=1相切于点B（2，1），且圆心的横坐标为1，则圆C被y轴截得的弦长为（　　）
A．
2
B．
2
2
C．1 D．2
组卷：81引用：3难度：0.7
解析
7．已知一条光线从点P（-1，5）射出，经直线x-y=0反射后经过点（2，3），则反射光线所在直线的方程为（　　）
A．2x+3y-13=0 B．3x+4y-17=0 C．4x+3y-17=0 D．3x+2y-12=0
组卷：21引用：2难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共6小题．解答应写出文字说明，证明过程或演算步骤，共70分）

21．已知双曲线C：
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）的离心率为
5
，右焦点F与点M（0，2
5
）的连线与其一条渐近线平行．
（1）求双曲线C的方程；
（2）经过点F的直线l与双曲线C的右支交于点A、B，试问是否存在一定点P，使∠OPA=∠OPB恒成立．若存在，请求出点P的坐标；若不存在，请说明理由．
组卷：97引用：3难度：0.5
解析
22．已知椭圆C：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的离心率为
3
2
，椭圆的上顶点B到两焦点的距离之和为4．
（1）求椭圆C的标准方程；
（2）若直线l：y=kx+m与椭圆C交于异于点B的两点P，Q，直线BP，BQ与x轴相交于M（x_M，0），N（x_N，0），若
1
x
M
+
1
x
N
=1，求证：直线l过一定点，并求出定点坐标．
组卷：451引用：5难度：0.5
解析