2022-2023学年浙江省北斗联盟高二（下）期中数学试卷

一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合

  A

  =

  {

  -

  2

  ，-

  1

  ，

  0

  ，

  1

  ，

  2

  }

  ，

  B

  =

  {

  x

  |

  -

  3

  ≤

  x

  ≤

  1

  }

  ，则A∩B=（　　）

  A．{-2，-1，0，1}	B．{-1，0，1}
  C．{0，1}	D．{-2，-1，0，1，2}
  组卷：82引用：3难度：0.8

  解析

• 2．设复数z满足z•（1+2i）=5，则z的虚部是（　　）

  A．2

  B．2i

  C．-2

  D．-2i
  组卷：186引用：10难度：0.8

  解析

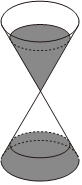• 3．沙漏是我国古代的一种计时工具，是用两个完全相同的圆锥顶对顶叠放在一起组成的（如右图）．在一个圆锥中装满沙子，放在上方，沙子就从顶点处漏到另一个圆锥中，假定沙子漏下来的速度是恒定的．已知一个沙漏中沙子全部从一个圆锥中漏到另一个圆锥中需总时长为1小时，当上方圆锥中沙子漏至圆锥高度的一半时，所需时间为（　　）

  A． 1 3 小时

  B． 7 8 小时

  C． 26 27 小时

  D． 8 9 小时
  组卷：141引用：8难度：0.6

  解析

• 4．平面向量

  a

  与

  b

  相互垂直，已知

  a

  =（6，-8），

  |

  b

  |

  =

  5

  ，且

  b

  与向量（1，0）的夹角是钝角，则

  b

  =（　　）

  A．（-3，-4）

  B．（4，3）

  C．（-4，3）

  D．（-4，-3）
  组卷：513引用：12难度：0.7

  解析

• 5．定义运算：

  a 1	a 2
  a 3	a 4

  =a₁a₄-a₂a₃，将函数f（x）=

  3	cos x 2
  1	sin x 2

  的图象向左平移m（m＞0）的单位后，所得图象关于y轴对称，则m的最小值是（　　）

  A． π 3

  B． 2 π 3

  C． 4 π 3

  D． 7 π 3
  组卷：82引用：6难度：0.9

  解析

• 6．概率论起源于博弈游戏.17世纪，曾有一个“赌金分配“的问题：博弈水平相当的甲、乙两人进行博弈游戏每局比赛都能分出胜负，没有平局．双方约定，各出赌金48枚金币，先赢3局者可获得全部赌金；但比赛中途因故终止了，此时甲赢了2局，乙赢了1局．向这96枚金币的赌金该如何分配？数学家费马和帕斯卡都用了现在称之为“概率“的知识，合理地给出了赌金分配方案．该分配方案是（　　）

  A．甲48枚，乙48枚	B．甲64枚，乙32枚
  C．甲72枚，乙24枚	D．甲80枚，乙16枚
  组卷：330引用：6难度：0.8

  解析

• 7．若a=log₂3，b=log₃4，c=log₄5，则a、b、c的大小关系是（　　）

  A．a＜b＜c

  B．b＜c＜a

  C．b＜a＜c

  D．c＜b＜a
  组卷：371引用：3难度：0.6

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知双曲线

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  过点

  M

  （

  3

  ，

  2

  ）

  ，且右焦点为F（2，0）．
  （1）求双曲线C的方程：
  （2）过点F的直线l与双曲线C的右支交于A，B两点，交y轴于点P，若

  PA

  =

  m

  AF

  ，

  PB

  =

  n

  BF

  ，求证：m+n为定值．
  （3）在（2）的条件下，若点Q是点P关于原点O的对称点，求三角形QAB的面积的取值范围．
  组卷：66引用：1难度：0.5

  解析

• 22．已知函数f（x）=alnx+

  1

  x

  ，a∈R．
  （1）当a=1时，求函数f（x）的单调区间；
  （2）若f（x）有经过原点的切线，求a的取值范围及切线的条数，并说明理由．
  （3）设函数g（x）=f（x）-x的两个极值点分别为x₁，x₂，且满足

  g

  （

  x

  1

  ）

  -

  g

  （

  x

  2

  ）

  x

  1

  -

  x

  2

  ≤

  2

  e

  e

  2

  -

  1

  a-2，求实数a的取值范围．
  组卷：255引用：2难度：0.3

  解析