2022-2023学年北京市顺义一中高二（下）月考数学试卷（3月份）

一、选择题（共10小题，每小题5分，满分50分）

• 1．在数列{a_n}中，a_n+1=a_n+2，且a₁=1，则a₄等于（　　）

  A．8

  B．6

  C．9

  D．7
  组卷：405引用：9难度：0.9

  解析

• 2．函数f（x）=

  x

  在x=1处的导数f′（1）等于（　　）

  A．- 1 2

  B． 1 2

  C．1

  D．2
  组卷：160引用：5难度：0.8

  解析

• 3．设等差数列{a_n}满足a₃=5，a₁₀=-9，S_n是数列{a_n}的前n项和，则使得S_n最大的序号n=（　　）

  A．4

  B．5

  C．6

  D．7
  组卷：437引用：9难度：0.9

  解析

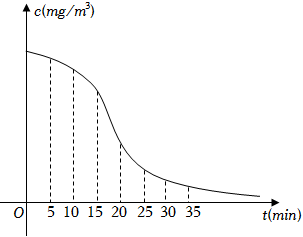• 4．降低室内微生物密度的有效方法是定时给室内注入新鲜空气，即开窗通风换气．在某室内，空气中微生物密度（c）随开窗通风换气时间（t）的关系如图所示，则下列时间段内，空气中微生物密度变化的平均速度最快的是（　　）

  A．[5，10]

  B．[5，15]

  C．[5，20]

  D．[5，35]
  组卷：251引用：5难度：0.7

  解析

• 5．四位同学返校看望老师，由于时间关系，只见到语文，数学，英语三位老师，于是他们邀请老师一起照相，三位老师坐中间共有多少种排列方式（　　）

  A．90

  B．120

  C．144

  D．216
  组卷：109引用：3难度：0.9

  解析

• 6．已知x=1是函数f（x）=x³-3ax+2的极小值点，那么函数f（x）的极大值为（　　）

  A．0

  B．1

  C．2

  D．4
  组卷：305引用：6难度：0.6

  解析

• 7．设数列{a_n}的前n项和为S_n，则“对任意n∈N*，a_n＞0”是“数列{S_n}为递增数列”的（　　）

  A．充分不必要条件

  B．必要不充分条件

  C．充分必要条件

  D．既不是充分也不是必要条件
  组卷：1127引用：6难度：0.7

  解析

三、解答题（共6小题，满分75分）

• 20．设函数f（x）=lnx+1，g（x）=ax+2，a∈R，记F（x）=f（x）-g（x）．
  （1）求曲线y=f（x）在x=1处的切线方程；
  （2）求函数F（x）的单调区间；
  （3）若函数f（x）=lnx+1的图象恒在g（x）=ax+2的图象的下方，求实数a的取值范围．
  组卷：191引用：5难度：0.6

  解析

• 21．已知有穷数列A：a₁，a₂，…，a_N（N∈N^*，N≥3）满足a_i∈{-1，0，1}（i=1，2，…，N）．给定正整数m,若存在正整数s,t（s≠t），使得对任意的k∈{0，1，2，…，m-1}，都有a_s+k=a_t+k，则称数列A是m-连续等项数列．
  （1）判断数列A：-1，1，0，1，0，1，-1是否为3-连续等项数列？是否为4-连续等项数列？说明理由；
  （Ⅱ）若项数为N的任意数列A都是2-连续等项数列，求N的最小值；
  （Ⅲ）若数列A：a₁，a₂，…，a_N不是4-连续等项数列，而数列A₁：a₁a₂，…，a_N，-1，数列A₂：a₁a₂，…，a_N，0与数列A₃：a₁，a₂，…，a_N，1都是4-连续等项数列，且a₃=0，求a_N的值．
  组卷：364引用：7难度：0.2

  解析