2023年广东省汕头市金山中学高考数学三模试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合A={x|2x-4＜0}，B={x|lgx＜1}，则A∩B=（　　）

  A．{x|x＜2}

  B．{x|x＜10}

  C．{x|0＜x＜2}

  D．{x|x＜0或x＞2}
  组卷：80引用：3难度：0.8

  解析

• 2．已知i是虚数单位，则复数

  z

  =

  2

  -

  i

  2022

  2

  +

  i

  2023

  对应的点所在的象限是（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：52引用：1难度：0.8

  解析

• 3．已知向量

  a

  =

  （

  -

  1

  ，

  1

  ）

  ，

  b

  =

  （

  3

  ，

  1

  ）

  ，则

  a

  在

  b

  上的投影向量为（　　）

  A．（1，0）	B． （ - 3 10 10 ，- 10 10 ）
  C． （ 1 ， 1 3 ）	D． （ - 3 5 ，- 1 5 ）
  组卷：401引用：9难度：0.6

  解析

• 4．如图的形状出现在南宋数学家杨辉所著的《详解九章算法•商功》中，后人称为“三角垛”．已知一个三角垛，最顶层有1个小球，第二层有3个，第三层有6个，第四层有10个，则第30层小球的个数为（　　）

  A．464

  B．465

  C．466

  D．467
  组卷：25引用：2难度：0.8

  解析

• 5．安排A，B，C，D，E，F共6名义工照顾甲、乙、丙三位老人，每两位义工照顾一位老人，考虑到义工与老人住址距离问题，义工A不安排照顾老人甲，则安排方法共有（　　）种．

  A．60

  B．61

  C．62

  D．63
  组卷：115引用：1难度：0.7

  解析

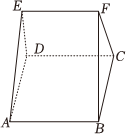• 6．如图，在多面体ABCDEF中，已知面ABCD是边长为3的正方形，EF∥AB，EF=

  3

  2

  ，EF与面AC的距离为2，则该多面体的体积为（　　）

  A． 9 2

  B．5

  C．6

  D． 15 2
  组卷：263引用：17难度：0.9

  解析

• 7．设过点P（-2，0）的直线l与圆C：x²+y²-4x-2y+1=0的两个交点为A，B，若8

  PA

  =5

  AB

  ，则|AB|=（　　）

  A． 8 5 5

  B． 4 6 3

  C． 6 6 5

  D． 4 5 3
  组卷：209引用：6难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知抛物线

  C

  1

  ：

  y

  2

  =

  4

  ax

  和

  C

  2

  ：

  x

  2

  =

  4

  y

  ，其中a＞0．C₁与C₂在第一象限内的交点为P．C₁与C₂在点P处的切线分别为l₁和l₂，定义l₁和l₂的夹角为曲线C₁、C₂的夹角．
  （1）若C₁、C₂的夹角为

  θ

  ，

  tanθ

  =

  3

  4

  ，求a的值；
  （2）若直线l₃既是C₁也是C₂的切线，切点分别为Q、R，当△PQR为直角三角形时，求出相应a的值．
  组卷：48引用：1难度：0.5

  解析

• 22．已知函数f（x）=e^x-axsinx-x-1，a∈R．
  （1）当a=0时，讨论函数f（x）的单调性；
  （2）当a=

  1

  2

  时，证明：对任意的x∈（0，+∞），f（x）＞0；
  （3）讨论函数f（x）在（0，π）上零点的个数．
  组卷：92引用：2难度：0.3

  解析